Função Exponencial: o que é, definição, propriedades e exemplos
A função exponencial é fundamental na matemática e aparece em diversos contextos, como crescimento populacional, juros compostos e processos físicos. Neste artigo, exploraremos suas definições, propriedades e aplicações práticas.
Definição
Dado um número real ![]() , tal que
, tal que ![]() , chamamos de função exponencial de base a a função
, chamamos de função exponencial de base a a função ![]() de
de ![]() que associa a cada
que associa a cada ![]() real o número
real o número ![]() .
.
Em símbolos:
![]() ,
,
![]() .
.
Exemplo de funções exponenciais:
a) ![]()
b) 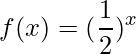
c) ![]()
d) ![]()
Propriedade 1:
Na função exponencial ![]() , temos
, temos
(1) ![]()
Veja demonstração intuitiva aqui.
Isso quer dizer que, o par ordenado ![]() pertence a função para todo
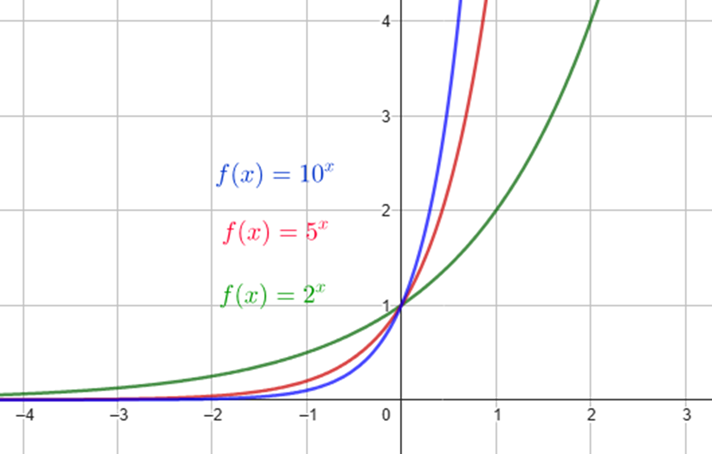
pertence a função para todo ![]() . Em outras palavras, o gráfico da função exponencial simples corta o eixo
. Em outras palavras, o gráfico da função exponencial simples corta o eixo ![]() no ponto ordenada
no ponto ordenada ![]() como mostra a seguinte figura.
como mostra a seguinte figura.
Propriedade 2:
A função exponencial ![]() , é crescente ou decrescente se, e somente se
, é crescente ou decrescente se, e somente se ![]() ou
ou ![]() . Portanto, dado os reais
. Portanto, dado os reais ![]() e
e ![]() , temos:
, temos:
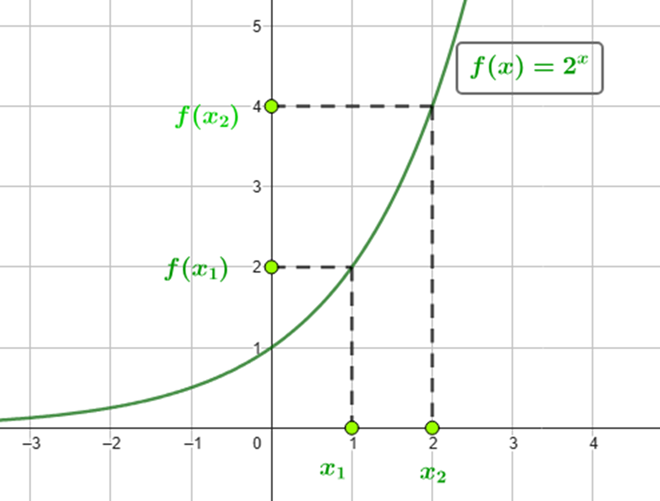
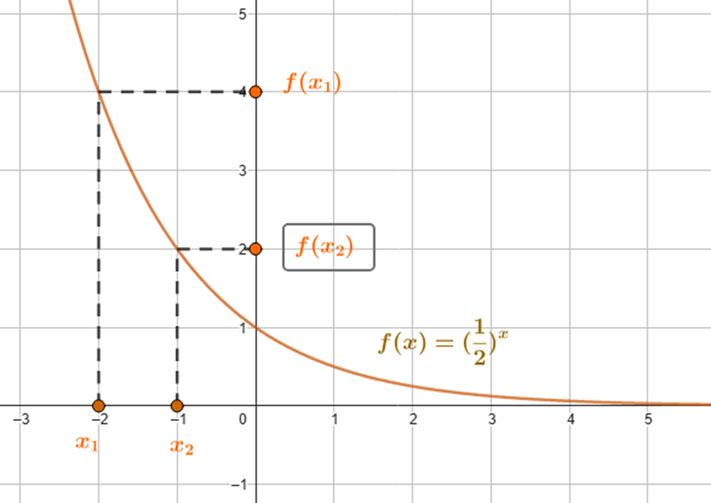
I) Crescente para ![]() :
:
![]()
veja o exemplo na seguinte imagem:
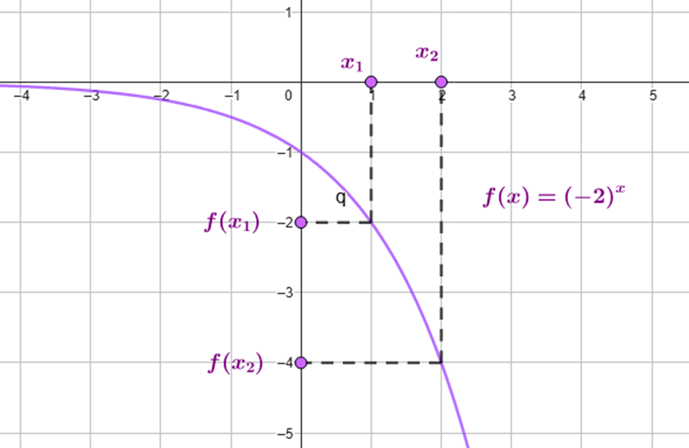
II) Decrescente para ![]() :
:
![]()
veja o exemplo na seguinte imagem:
ou
Propriedade 3:
3) A função exponencial ![]() , com
, com ![]() , é injetora, pois, dados
, é injetora, pois, dados ![]() e
e ![]() tais que
tais que ![]() por exemplo
por exemplo ![]() , vem:
, vem:
I) Se ![]() , temos:
, temos: ![]() ;
;
I) Se ![]() , temos:
, temos: ![]() .
.
Em outras palavras, é uma função que não repete valores de imagem
📌 Aplicações da Função Exponencial na Vida Real
A função exponencial não é apenas um conceito teórico — ela aparece em diversas áreas da matemática aplicada e da vida cotidiana. Veja alguns exemplos:
- Finanças: é usada para calcular juros compostos, crescimento de investimentos e evolução de dívidas ao longo do tempo;
- Biologia: modela o crescimento populacional de organismos e a disseminação de vírus;
- Física e Química: aparece em processos como decaimento radioativo e resfriamento de corpos;
- Tecnologia: descreve o crescimento exponencial de dados em algoritmos e inteligência artificial;
- Engenharia e Demografia: é usada para prever o crescimento de cidades e demandas de energia.
Por isso, entender a função exponencial é fundamental não só para provas e vestibulares, mas também para compreender o mundo ao nosso redor — onde o crescimento rápido e os processos contínuos estão presentes em diversas situações.