Exemplos de Indeterminação no cálculo dos Limites
Neste post apresentam-se Exemplos de Indeterminação no cálculo dos Limites, sendo uma continuação do post anterior, na qual introduzimos o conteúdo da Indeterminação nos limites.
Exemplo 1 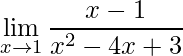
Sempre que vamos resolver um limite quando ![]() tende a um valor finito de um polinômio ou divisão de polinômios, o primeiro passo é verificar se a aplicação do limite no próprio ponto nos dá uma resposta (Propriedade dos Limites nº10) , ou seja:
tende a um valor finito de um polinômio ou divisão de polinômios, o primeiro passo é verificar se a aplicação do limite no próprio ponto nos dá uma resposta (Propriedade dos Limites nº10) , ou seja:
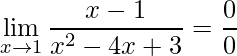 .
.
Aqui encontra-se um dos casos de indeterminação nos limites. Assim, para superar esta indeterminação, propõe-se utilizar o método de decompor a expressão do denominador como produto de suas raízes. Assim, caso uma das suas raízes seja igual ao numerador, então se simplifica.
Para encontrar as raízes podemos utilizar a Formula de Bhaskara ou Soma e Produto ou até mesmo o algoritmo de Briot-Ruffini, logo encontram-se as raízes 1 e 3. Assim, tem-se:
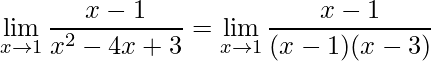 .
.
Simplificando os termos iguais encontramos facilmente o limite dado por:
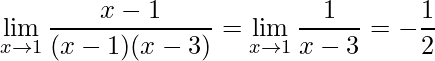 .
.
Exemplo 2 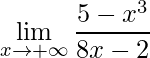
Neste exemplo, utiliza-se outra estratégia que também poderia ser usada no exemplo anterior, que é dividir a expressão do numerador e do denominador por ![]() :
:
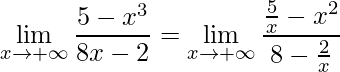 .
.
Portanto, aplicando o limite tem-se:
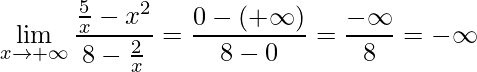 .
.
Exemplo 3 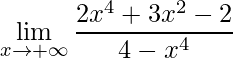
Desenvolvendo a mesma metodologia do exemplo anterior, no entanto dividindo por ![]() tem-se:
tem-se:
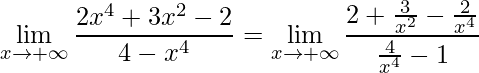 .
.
Portanto, aplicando o limite fica-se com:
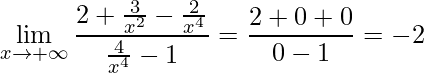 .
.
Exemplo 4 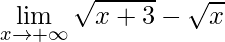
Aplicando diretamente o limite temos outro tipo de indeterminação da forma:
![]() .
.
Para superar esta indeterminação propõe-se utilizar a racionalização, que consiste em multiplicar o numerador e denominador pelo conjugado do numerador. Assim, tem-se:
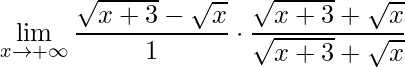 ,
,
que resulta em:
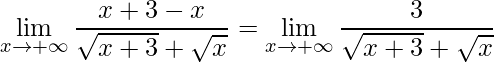 .
.
Fazendo um cálculo direto aplicando o limite tem-se:
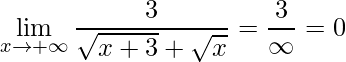 .
.
Portanto, espero que tenha gostado desses Exemplos de Indeterminação no cálculo dos Limites. Continuem nos acompanhando. Compartilhem esse post com os amigos. Divulguem nosso site. Além disso, se ficou alguma duvida, comente abaixo usando seu login do Facebook. Por fim, assista a resolução de outros exemplos em vídeo clicando aqui.


Deixe um comentário