Estudo do sinal da função
O Estudo do sinal da função consiste em avaliar o comportamento da função ao longo do domínio, ou seja, descrever onde ela é crescente, decrescente e os pontos de inflexão.
Para realizar este estudo utilizamos os conhecimentos de derivada, uma vez que a derivada descreve a inclinação da reta tangente. Assim, quando tem-se:
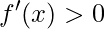, a inclinação é positiva então a função é crescente.
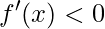, a inclinação é negativa então a função é decrescente.
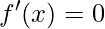, a inclinação é nula então a função está nos pontos de inflexão.
Vejamos um exemplo:
Dada a função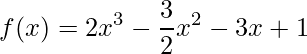 
, faça o estudo da função.
Primeiramente deve-se derivar a função f(x). Como se trata de um polinômio pode-se aplicar a derivada da potência em cada termo, onde obtém-se:
.
Iniciamos encontrando os pontos de inflexão, pontos onde a derivada é igual a zero, ou seja, onde a inclinação da reta tangente é nula.
Como se trata de uma equação do segundo grau pode-se encontrar as raízes aplicando a fórmula de Bhaskara, onde encontram-se as raízes:
e 
.
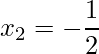Isto quer dizer que os pontos 
e 
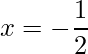a função f(x) não é crescente nem decrescente.
Conhecidos os pontos de inflexão, deve-se determinar onde a função f(x) é crescente e decrescente.
Pode-se fazer de duas formas:
1) Uma vez conhecidos o comportamento de uma função cúbica e os pontos de inflexão, tem-se informações suficientes para descrever os sinais da função.
2) Uma vez não conhecidos, deve-se encontrar onde a função é crescente, , e decrescente, .
Começamos com o caso onde a função é crescente () :
.
Note que pode-se escrever na forma do produto das raízes da diferença como:
.
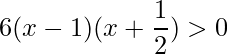Aplicando o conhecimento de inequação encontra-se que a função é crescente em:
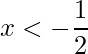e 
.
De forma análoga, pode-se encontrar onde ela é decrescente, :
.
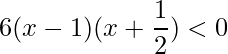Resolvendo a inequação encontra-se:
.
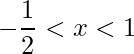Observa-se no gráfico o comportamento da função conforme acabamos de encontrar.
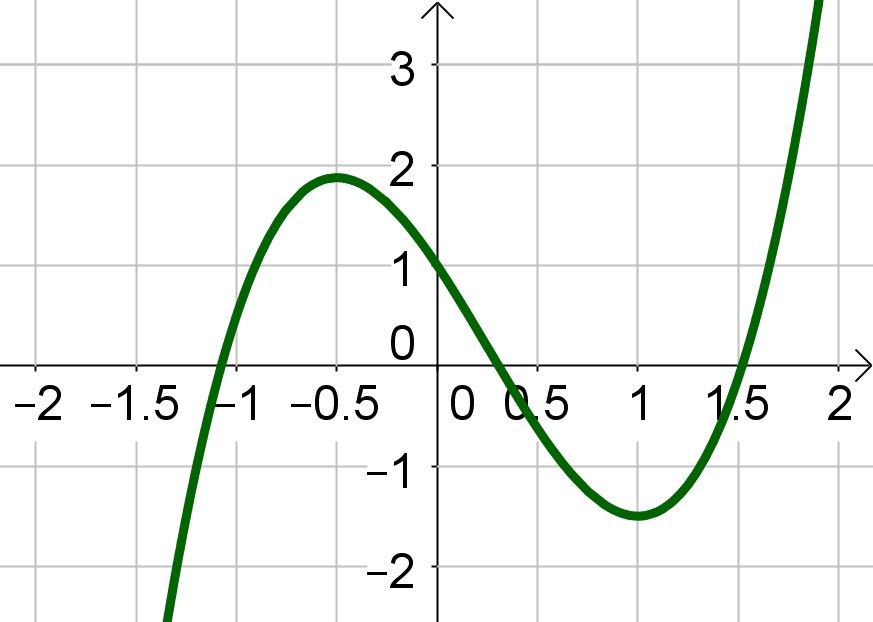
Pode-se também perceber que os pontos de inflexão são pontos de máximo local em 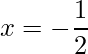e mínimo local em 
. Assista um exemplo em vídeo clicando aqui.
