Diferenciabilidade de uma função
A Derivabilidade ou Diferenciabilidade de uma função é a analise feita para saber se uma função derivada está definida em todos os pontos do seu domínio.
Definição: Uma função é derivável ou diferenciável no ponto ![]() , se existir o limite:
, se existir o limite:
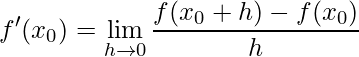 .
.
Se ![]() for derivável em todos os pontos de um intervalo aberto
for derivável em todos os pontos de um intervalo aberto ![]() , então
, então ![]() é derivável em
é derivável em ![]() .
.
Caso seja derivável em todos os pontos do intervalo ![]() , então
, então ![]() é derivável em toda parte.
é derivável em toda parte.
Há algumas situações em que uma função mesmo sendo continua em ![]() , ainda assim não é derivável em
, ainda assim não é derivável em ![]() . Essas situações são chamadas de:
. Essas situações são chamadas de:
- pontos de bico;
- pontos de tangência vertical.
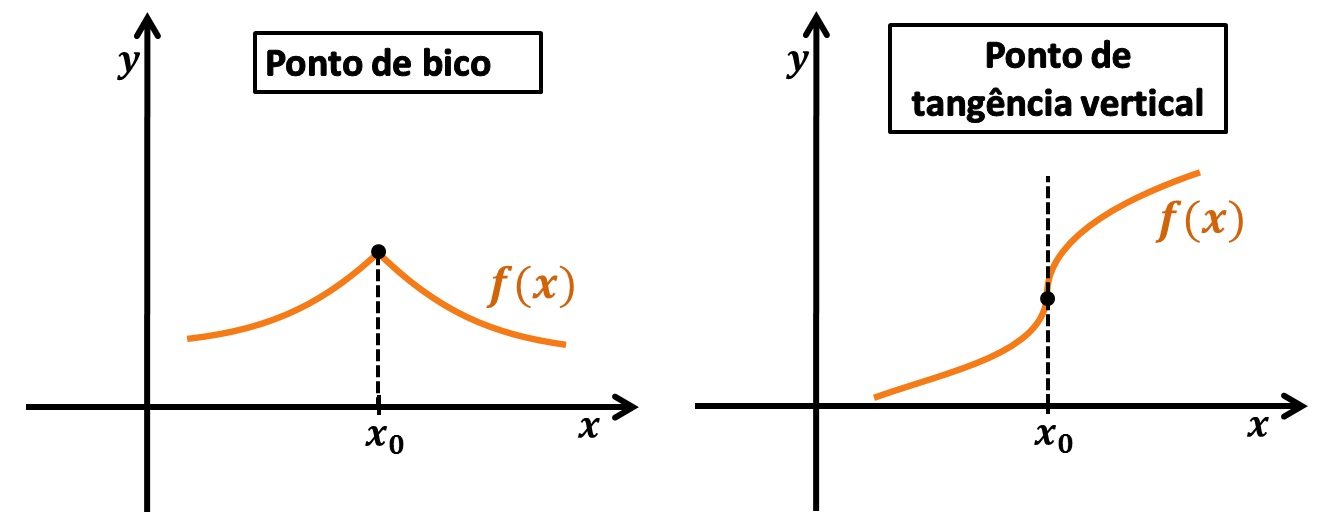
Nos pontos de bico os limites laterais da definição das derivadas são distintos e nos pontos de tangência vertical as inclinações da reta secante pela direita e pela esquerda são ![]() ou
ou ![]() ou vice-versa.
ou vice-versa.
Obs: Mas se uma função é diferenciável em ![]() , então ela é continua em
, então ela é continua em ![]() .
.
Exemplo: Determine se a função é diferenciável
Aplicando os limites laterais percebemos facilmente que a função é continua, mas isto não é suficiente, devemos aplicar o limites laterias da definição formal.
- Na esquerda
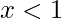 :
:
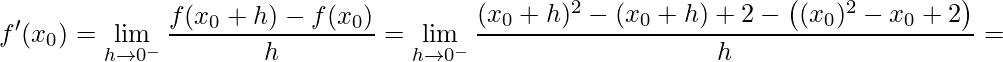
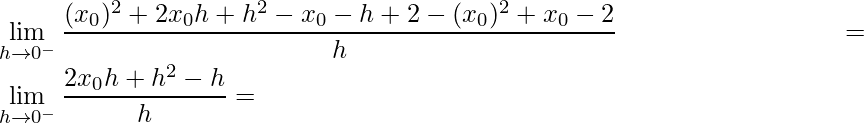
![]() .
.
Assim, tem-se que ![]() é diferenciável.
é diferenciável.
- Na direita
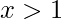 :
:
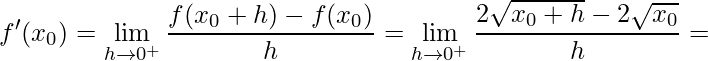
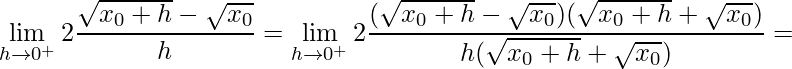
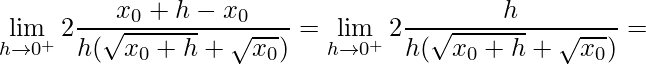
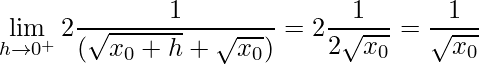 .
.
Assim, tem-se que ![]() é diferenciável.
é diferenciável.
- No ponto
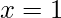 :
:
No ponto utiliza-se o mesmo cálculo feito em ambos os lados, assim tem-se:
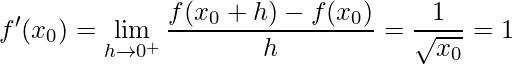
e
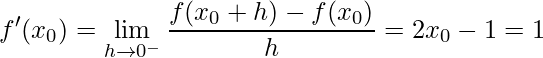 .
.
Portanto, percebe-se que ambos os lados possuem mesmo limite.
Conclusão, ![]() é diferenciável para todo valor de
é diferenciável para todo valor de ![]() .
.
Acompanhe também a explicação em vídeo clicando aqui.

