Exemplos das propriedades das derivadas

Primeiros exemplos: aplicando as propriedades das derivadas

 

Uma vez apresentado as propriedades das derivadas vamos aplicá-las em alguns exercícios. O objetivo aqui apresentar exemplos das propriedades das derivadas.

Em todos os exemplos a seguir encontra-se a função derivada das funções apresentadas:

a) h(x)=2x^{3}+4x-8

Neste exemplo utiliza-se a propriedade que diz: a derivada da soma/subtração  é a soma/subtração das derivadas. 

\displaystyle\frac{d}{dx}\big[2x^{3}+4x-8\big]=\frac{d}{dx}\big[2x^{3}\big]+\frac{d}{dx}\big[4x\big]-\frac{d}{dx}\big[8\big] .

Em seguida, na primeira e segunda derivada usa-se a propriedade do produto por uma constante e a propriedade da potência e na terceira derivada a propriedade da constante, assim obtém-se: 

\displaystyle\frac{d}{dx}\big[2x^{3}\big]+\frac{d}{dx}\big[4x\big]-\frac{d}{dx}\big[8\big]=6x^{2}+4-0=6x^{2}+4 . 

Clique aqui para ver em vídeo outro exemplo.

b) h(x)=(x^{2}-3)(x+2) 

Neste exemplo pode-se fazer a multiplicação dos dois termos e derivar da mesma maneira que resolvemos o exemplo anterior, mas como queremos utilizar a propriedade do produto faz-se de outra forma. Assumi-se que:

f(x)=x^{2}-3 ;

g(x)=x+2 .

Assim, tem-se h(x)=f(x)\cdot g(x) e aplicando a propriedade do produto fica-se com: 

\displaystyle\frac{d}{dx}\bigg[(x^{2}-3)(x+2)\bigg]=(x+2)\cdot\frac{d}{dx}\big[x^{2}-3\big]+(x^{2}-3)\cdot\frac{d}{dx}\big[x+2\big]= 

\displaystyle (x+2)\cdot2x+(x^{2}-3)\cdot 1=2x^{2}+4x+x^{2}-3=3x^{2}+4x-3 .

Pela multiplicação tem-se: 

h(x)=(x^{2}-3)(x+2)=x^{3}+2x^{2}-3x-6 .

Aplicando a derivada e resolvendo encontra-se a mesma resposta: 

\displaystyle \frac{d}{dx}\big[x^{3}+2x^{2}-3x-6\big]=3x^{2}+4x-3 . 

Clique aqui para ver em vídeo outro exemplo em que utilizam a derivada do produto.

c) 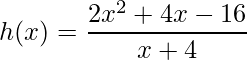\displaystyle h(x)=\frac{2x^{2}+4x-16}{x+4}

Neste exemplo utiliza-se a propriedade da divisão onde assumi-se que:

f(x)=2x^{2}+4x-16

g(x)=x+4 .

Portanto, tem-se: 

\displaystyle \frac{d}{dx}\Bigg[\frac{2x^{2}+4x-16}{x+4}\Bigg]=\frac{(x+4)\cdot\frac{d}{dx}\big[2x^{2}+4x-16\big]-(2x^{2}+4x-16)\cdot\frac{d}{dx}\big[x+4\big]}{(x+4)^{2}} .

Aplicando as derivadas nos termos indicados obtém-se:

\displaystyle \frac{(x+4)\cdot(4x+4)-(2x^{2}+4x-16)\cdot1}{(x+4)^{2}}=\frac{2x^{2}+16x+32}{x^{2}+8x+16}=2 . 

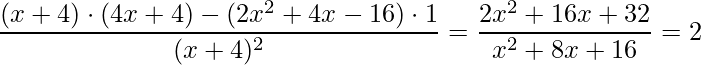Clique aqui para ver em vídeo outro exemplo em que utilizam a derivada da divisão.

d) \displaystyle h(x)=\sqrt{x^{4}+2x^{2}+4}

Neste exemplo pode-se perceber que tem-se uma função composta, na verdade, uma função raiz composta por uma função polinomial. Quando temos que  derivar funções compostas pode-se utilizar a Regra da cadeia.

Assumindo que

f(u)=\sqrt{u} 

g(x)=x^{4}+2x^{2}+4 ,

tem-se:

\displaystyle \frac{d}{dx}\Bigg[\sqrt{x^{4}+2x^{2}+4}\Bigg]=\frac{d}{du}\Big[\sqrt{u}\Big]\cdot\frac{d}{dx}\Big[x^{4}+2x^{2}+4\Big]= 

\displaystyle \frac{1}{2}\frac{1}{\sqrt{u}}\cdot\Big(4x^{3}+4x\Big) .

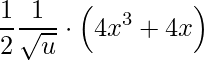substituindo a função u no resultado e simplificando obtém-se:

\displaystyle \frac{1}{2}\frac{(4x^{3}+4x)}{\sqrt{x^{4}+2x^{2}+4}}=\frac{2x^{3}+2x}{\sqrt{x^{4}+2x^{2}+4}} .

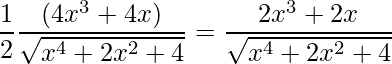Clique aqui ou aqui para ver outros exemplos das propriedades das derivadas em vídeo em que utiliza-se a regra da cadeia.