Exemplos das principais derivadas
Neste post resolve-se alguns Exemplos das principais derivadas, onde utilizam-se as derivadas apresentadas na Tabela anterior.
Encontre a derivada das seguintes funções:
a) 
Pode-se perceber que esta função e composta pelo produto de dois termos, por isto aplica-se a derivada do produto, onde obtém-se:
![\displaystyle y'=\frac{d}{dx}\Big[x^{3}\Big]sen^{2}(5x)+\frac{d}{dx}\Big[sen^{2}(5x)\Big]x^{3}](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-9f7ee9d0e3f32f7f2c066e1c13e80cac_l3.png "Rendered by QuickLaTeX.com")
.
Para explicar de forma mais clara, dividi-se esta questão em duas. Na primeira derivada aplica-se a regra da potência
.
Na segunda deve-se utilizar a regra da cadeia
![\displaystyle y'=2sen(5x)\frac{d}{dx}\Big[sen(5x)\Big]x^{3}](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-f14a28a2b407372888fe20c12ca8924f_l3.png "Rendered by QuickLaTeX.com")
e, em seguida, fazer uma substituição de variável, 
, assim:
.
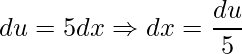Substituindo tem-se:
![\displaystyle y'=2sen(5x)\frac{d}{\frac{du}{5}}\Big[sen(u )\Big]x^{3}=10sen(5x)\frac{d}{du}\Big[sen(u )\Big]x^{3}](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-b5459fdf219eacf3296382e696ae5015_l3.png "Rendered by QuickLaTeX.com")
.
Aplicando a derivada da função seno presente na tabela e substituindo o valor de u, obtém-se:
.
Para finalizar basta somar as duas partes para encontrar:
.
b) 
Novamente deve-se utilizar a regra da cadeia:
![\displaystyle y'=-sen\big(a^{x^{2}}\big)\frac{d}{dx}\Big[a^{x^{2}}\Big]](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-7dda721ae75755f23581fe64bde9af00_l3.png "Rendered by QuickLaTeX.com")
.
Aplicando a derivada da função exponencial contida na tabela fica-se com:
![\displaystyle y'=-sen\big(a^{x^{2}}\big)a^{x^{2}}\ln a \frac{d}{dx}\Big[x^{2}\Big]](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-0435253872bb56abb5c7ce9a4a70ae38_l3.png "Rendered by QuickLaTeX.com")
.
Derivando obtém-se:
.
c) 
Aplicando a derivada da função logaritmo natural tem-se:
![\displaystyle y'=\frac{\frac{d}{dx}\big[sec(x)\big]}{sec(x)}](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-e9c47d92bd85adac04a2ce2a778eae77_l3.png "Rendered by QuickLaTeX.com")
.
Aplicando a derivada de secante fica-se com:
![\displaystyle y'=\frac{sec(x)tg(x)\frac{d}{dx}\big[x\big]}{sec(x)}](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-274001b4fceeafb9dffa6d908f9f2425_l3.png "Rendered by QuickLaTeX.com")
.
Aplicando a derivada de x e simplificando obtém-se:
.
Veja outros exemplos resolvidos clicando aqui.
