Domínio e Imagem – Conjuntos de entrada e saída
O conceito de Domínio e Imagem é fundamental para o estudo de funções, pois representam os conjuntos de entrada e saída, respectivamente, de uma função. Eles podem ser conceituados da seguinte forma:
1) Domínio: é o conjunto de todas as possíveis entradas, ou seja, é o conjunto de todos os valores nas quais a variável independente, $latex x&s=1$, pode assumir.
2) Imagem: é o conjunto de todas as saídas oriundas do conjunto das entradas, ou seja, é o conjunto que possui a variável dependente $latex f(x)&s=1$, que tem sua origem em $latex x&s=1$.
Obs: A imagem não é necessariamente igual ao contradomínio. O contradomínio é o conjunto de saídas, ou seja, contém toda a imagem, mas pode conter também outros elementos.
Uma função $latex f&s=1$ com domínio $latex x&s=1$ e imagem $latex f(x)&s=1$ podem ser projetados graficamente em um plano cartesiano, na qual ![]() .
.
Exemplos: Clique nos exemplos e veja suas resoluções.
Calcule o domínio e a imagem sabendo que ![]() .
.
Ex 1) ![]() .
.
Ex 2) ![]() .
.
Ex 3) ![]() .
.
Ex 4) 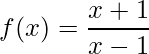 .
.

