Integrais

Integrais – Cálculo de Áreas

O cálculo integral tem como sua finalidade originária encontrar área de região plana sob uma curva no plano cartesiano, onde estas curvas são definidos por funções. Por exemplo, na figura a seguir temos uma área A em que seu contorno é formado pela função f(x) e as retas x=a, x=b e y=0 (eixo x).

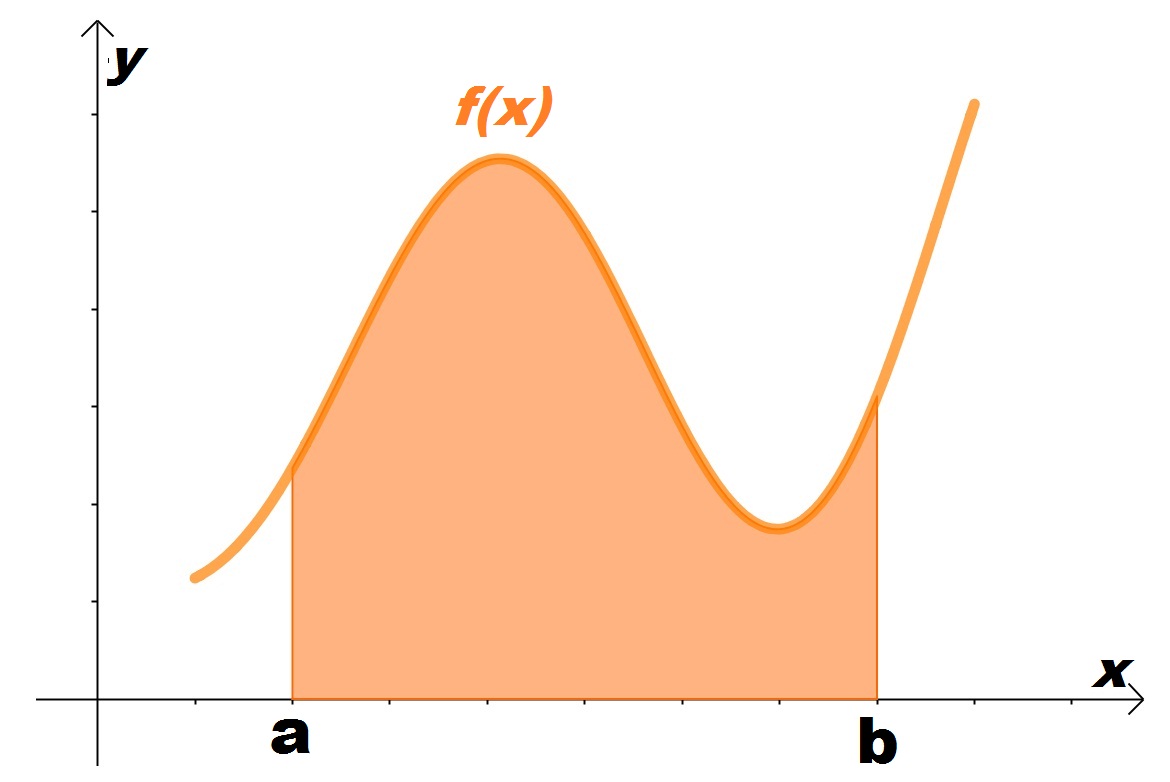
Esta área A é representada da seguinte forma

. 

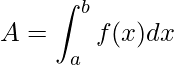Integral de Riemann

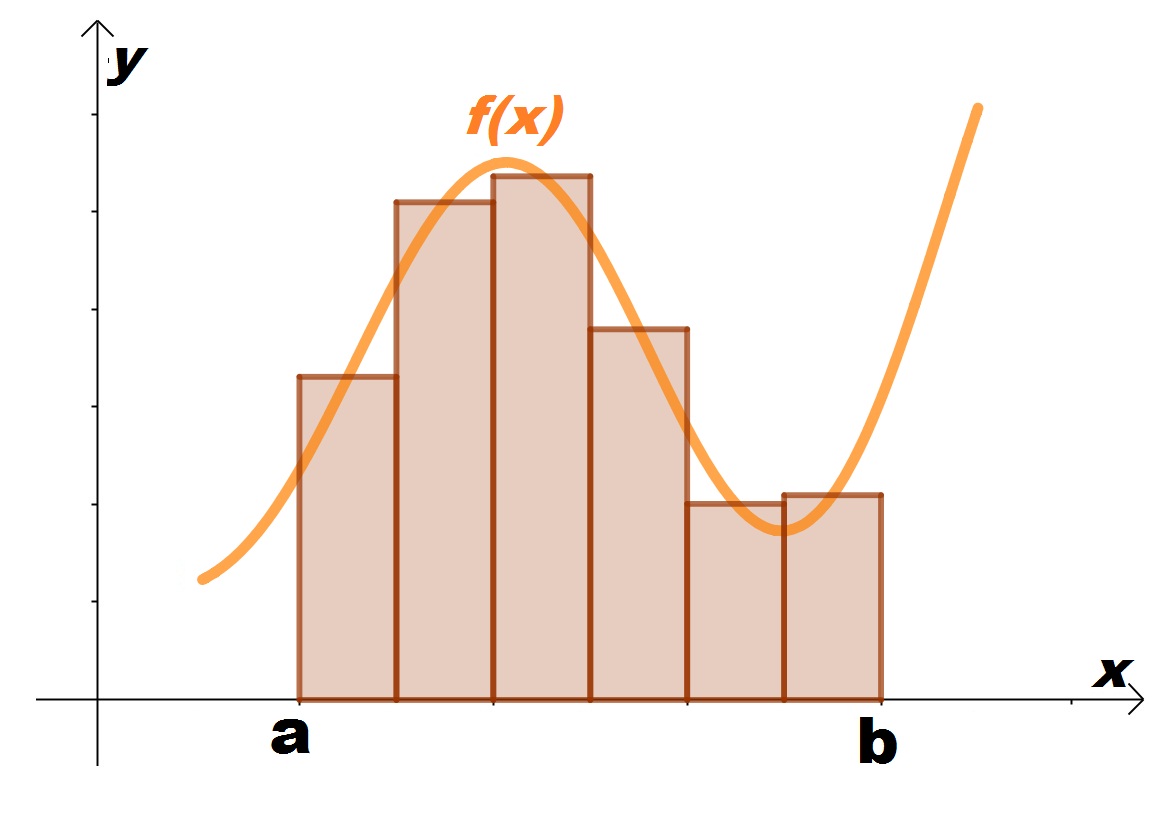
O primeiro a apresentar uma definição de integral foi Bernhard Riemann, por isto chamamos de integral de Riemann. Ele partiu de uma ideia intuitiva de calcular esta área A aproximando-a por áreas de retângulos, ou seja, ele particionou o intervalo e com cada parte construiu retângulos com altura  para .

Chamando cada intervalo da partição de  e para cada altura dos retângulos de  temos 

.

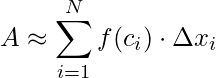Perceba que quanto mais partições forem feitas, os retângulos melhor preenchem a área sob a curva e menor será as sobras sobre a curva, assim minimizando o erro. Portanto, se fizermos , as espessuras dos retângulos tentem a zero e também o erro tenderá a zero. Desta forma obtém-se área desejada

.

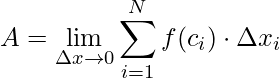Perceba que ao tender a zero, significa dizer que os intervalos tornam-se cada vez menores, ou seja, seu comprimento torna-se infinitesimal, que em linguagem matemática é simbolizado por .  

Portanto, para esta soma Riemann chamou de integral e representou da forma que hoje conhecemos 

. 

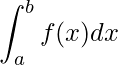Em breve começaremos a publicar mais materiais sobre Integrais, continue acompanhando.