Integração por Partes: a antiderivada da Regra do Produto

No cálculo integral há basicamente duas técnicas de integração: Integração por Substituição e Integração por Partes. Esta última será o tema deste post, onde iniciaremos fazendo uma pequena dedução da fórmula. A base desta dedução vem da Regra do Produto vista na diferenciação. Em seguida, apresentaremos uma exemplo resolvido passo a passo.

Como motivação, observe a seguinte integral e perceba que nesta não podemos aplicar as fórmulas das integrais imediadas nem a Integração por Substituição

$\displaystyle \int 4xe^{x}dx$ .

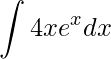Assim precisamos utilizar alguma outra metodologia que transforme a integral dada por outra em que conhecemos sua integral imediata.

Dedução da Integração por Partes

Como já anunciamos na introdução deste post, a dedução da Integração por Parte tem sua base na Regra do Produto. A Regra do Produto nos diz que:

Se as funções $f(x)$ e $g(x)$ possuírem derivadas no intervalo aberto $(a,b)$ então a função $f(x)\cdot g(x)$ possui derivada em $(a,b)$ e

$\displaystyle \frac{d}{dx}\big[f(x)\cdot g(x)\big]=g(x)\cdot\frac{d}{dx}\big[f(x)\big]+f(x)\cdot \frac{d}{dx}\big[g(x)\big]$ .

Tomando esta expressão e integrando ambos os lados teremos

$\displaystyle \int \bigg(\frac{d}{dx}\big[f(x)\cdot g(x)\big]\bigg)dx=\int \bigg(g(x)\cdot\frac{d}{dx}\big[f(x)\big]+f(x)\cdot \frac{d}{dx}\big[g(x)\big]\bigg)dx$

assim

$\displaystyle f(x)\cdot g(x)+C=\int \bigg(g(x)\cdot\frac{d}{dx}\big[f(x)\big]+f(x)\cdot \frac{d}{dx}\big[g(x)\big]\bigg)dx$ .

Aplicando no lado direito da igualdade a propriedade da soma das integrais

$\displaystyle f(x)\cdot g(x)+C=\int g(x)\cdot\frac{d}{dx}\big[f(x)\big]dx+\int f(x)\cdot \frac{d}{dx}\big[g(x)\big]dx$ .

Por fim, basta isolar uma das duas integrais

$\displaystyle \int f(x)\cdot \frac{d}{dx}\big[g(x)\big]dx=f(x)\cdot g(x)-\int g(x)\cdot\frac{d}{dx}\big[f(x)\big]dx+C$ .

Perceba que a integral à direita produzirá uma nova constante, assim não é necessário manter a constante. E com a finalidade de “limpar” a notação trocaremos a escrita das derivadas

$\displaystyle\int f(x)g'(x)dx=f(x)g(x)-\int g(x)f'(x)dx$ .

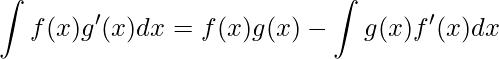Observação 1: tradicionalmente utiliza-se a notação da Integração por Partes com as funções u(x) e v(x). Tomando u(x)=f(x) e v(x)=g(x), derivando ambas temos du=f'(x)dx e dv=g'(x)dx, substituindo na fórmula a cima

$\displaystyle\int u(x)dv=u(x)v(x)-\int v(x)du$ .

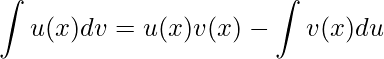Observação 2: a ordem em que aparecem as funções no integrando não determinam a escolha da função u(x) e v(x).

Exemplo resolvido passo a passo de Integração por Partes

Determine a seguinte integral utilizando Integração por Partes:

$\displaystyle \int 4xe^{x}dx$

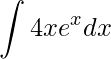
Dica: Se no integrando tiver uma função polinomial, a melhor escolha é tomá-la como a função u(x). O motivo é que ao derivar ela reduzirá sua ordem, enquanto que integrar aumentará.

Definidas as funções u(x) e dv, devemos derivar a primeira e integral a segunda, onde teremos

$\displaystyle u(x)=4x$ assim $\displaystyle du=4dx$

$\displaystyle dv=e^{x}dx$ assim $\displaystyle v=e^{x}$ .

O próximo passo é substituir todos estes termos na fórmula da Integração por Partes

$\displaystyle \int 4xe^{x}dx=4xe^{x}-\int e^{x}4dx$ .

Perceba que a integral que surgiu conhecemos sua integral imediata, logo a dificuldade do problema foi superada. Aplicando a integral imediata do segundo termo da direita temos a solução

$\displaystyle \int 4xe^{x}dx=4xe^{x}-4e^{x}+C$ .

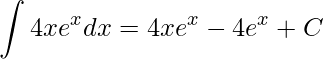Observação: Em muitas integrais temos a necessidade de aplicar mais de uma vez a Integração por Partes. Por exemplo, se a integral que acabamos de resolver tivesse uma função polinomial de 2ª ordem.

Veja outros exercícios resolvidos clicando aqui ou aqui.