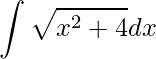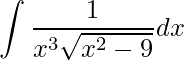Integração por Substituição Trigonométrica

Integração por Substituição Trigonométrica 

O método da Integração por Substituição Trigonométrica é utilizado para resolver integrais em que seu integrando contém uma destas três expressões algébricas:  

\displaystyle \sqrt{a^{2}-x^{2}}, \displaystyle \sqrt{a^{2}+x^{2}} ou \displaystyle \sqrt{x^{2}-a^{2}} 

onde a é uma constante positiva. O método tem como base a substituição destas expressões algébricas por expressões trigonométricas. Por sua vez, as expressões trigonométricas são encontradas nos triângulos retângulos através do Teorema de Pitágoras. Onde seus lados são a, x e o termo raiz, que conforme o caso, assume diferentes lados do triângulo. 

Em primeiro lugar, queremos apresentar os 3 casos das expressões algébricas e para cada uma deles, as relações necessárias para substituição, que são a variável x, o termo dx e o termo raiz. Em seguida, resolveremos alguns exemplos.  

Tipo 1: \displaystyle \sqrt{a^{2}-x^{2}}

Integração por Substituição Trigonométrica - Tipo 1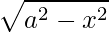

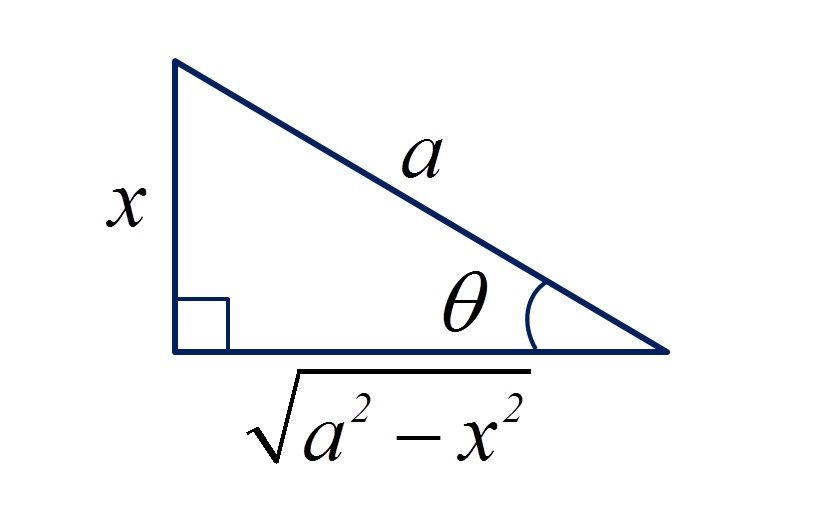
No primeiro tipo, utilizamos a relação trigonométrica do seno. Assim, 

\displaystyle x=a\cdot sen(\theta )

e derivando 

\displaystyle dx=a\cdot cos(\theta )d\theta.

Entretanto, para o radical termos que utilizar a relação cosseno

\displaystyle \sqrt{a^{2}-x^{2}}=a\cdot cos(\theta ).

Tipo 2: \displaystyle \sqrt{a^{2}+x^{2}}

Integração por Substituição Trigonométrica - Tipo 2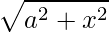

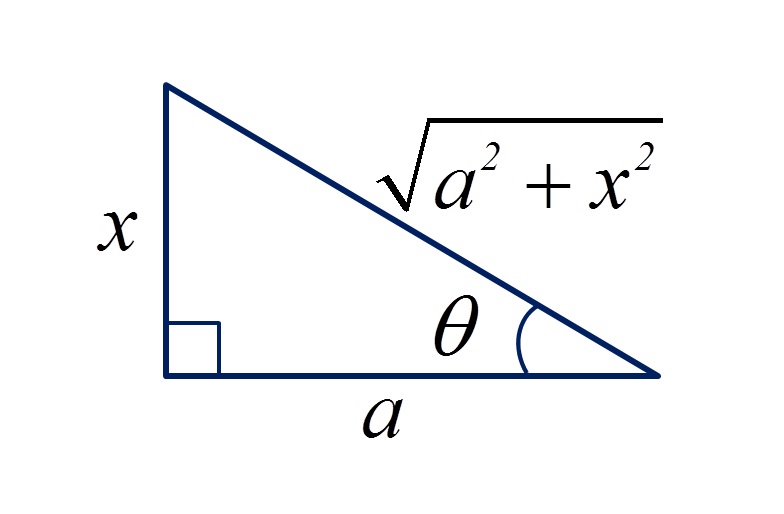
No segundo tipo, utilizamos a relação trigonométrica da tangente. Assim sendo, temos

\displaystyle x=a\cdot tg(\theta )

e derivando 

\displaystyle dx=a\cdot sec^{2}(\theta )d\theta.

Entretanto, para o radical termos que utilizar a relação secante, que é 1 sobre cosseno

\displaystyle \sqrt{a^{2}+x^{2}}=a\cdot sec(\theta ).

Tipo 3: \displaystyle \sqrt{x^{2}-a^{2}}

Integração por Substituição Trigonométrica - Tipo 3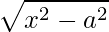

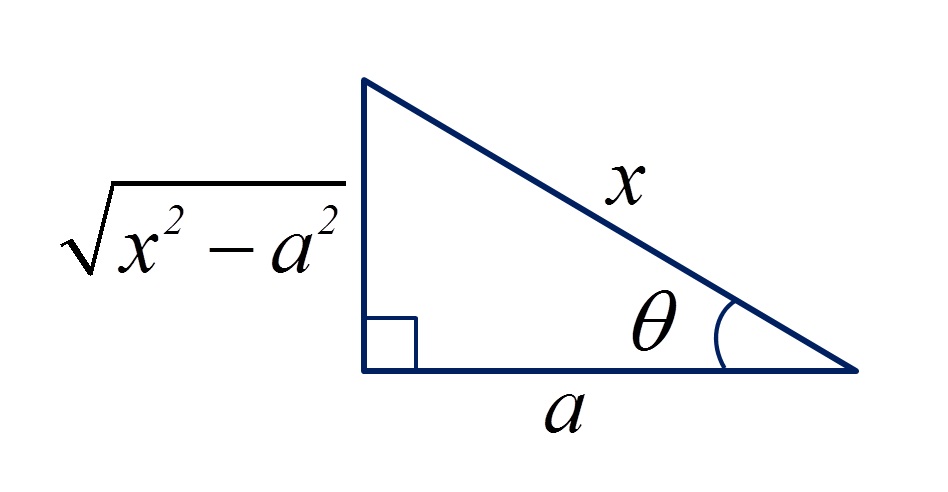
No terceiro tipo, utilizamos a relação trigonométrica do secante. Dessa forma, temos 

\displaystyle x=a\cdot sec(\theta )

e derivando 

\displaystyle dx=a\cdot sec(\theta )\cdot tg(\theta )d\theta.

Entretanto, para o radical termos que utilizar a relação tangente

\displaystyle \sqrt{x^{2}-a^{2}}=a\cdot tg(\theta ). 

Exemplos resolvidos de Integração por Substituição Trigonométrica

Resolva as seguintes integrais:

1)\displaystyle \int\frac{\sqrt{9-x^{2}}}{x^{2}}dx. 

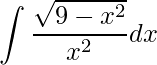Antes de tudo, devemos identificar qual tipo de relações que devemos utilizar. Neste caso, o termo raiz é do primeiro tipo, então 

\displaystyle x=3sen(\theta ).

Visto que o denominador é dado por \displaystyle x^{2}, precisamos elevar a expressão anterior ao quadrado, assim

\displaystyle x^{2}=9sen^{2}(\theta ).

Precisamos também da derivada

\displaystyle dx=3cos(\theta )d\theta

e do termo raiz

\displaystyle \sqrt{9-x^{2}}=3cos(\theta ).

Obtido todos os termos necessários, devemos substituir 

\displaystyle \int\frac{\sqrt{9-x^{2}}}{x^{2}}dx=\int \frac{3cos(\theta )}{9sen^{2}(\theta )}3cos(\theta )d\theta=\int \frac{cos^{2}(\theta )}{sen^{2}(\theta )}d\theta.

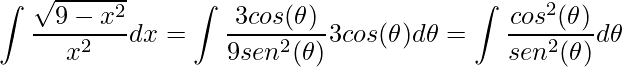Relembre que

\displaystyle \frac{cos^{2}(\theta )}{sen^{2}(\theta )}=cotg^{2}(\theta )=cossec^{2}(\theta )-1,

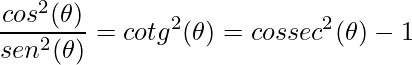fizemos esta última igualdade, pois a integral de cossecante ao quadrado é tabelada. Assim

\displaystyle \int\frac{\sqrt{9-x^{2}}}{x^{2}}dx=\int cossec^{2}(\theta )-1d\theta

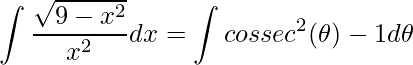
Integrando teremos 

\displaystyle \int cossec^{2}(\theta )-1d\theta=-cotg(\theta )-\theta +C.

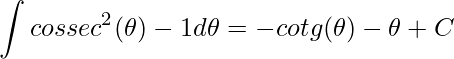Como 

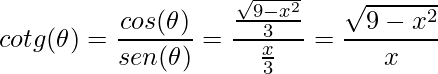
\displaystyle cotg(\theta )=\frac{cos(\theta )}{sen(\theta )}=\frac{\frac{\sqrt{9-x^{2}}}{3}}{\frac{x}{3}}=\frac{\sqrt{9-x^{2}}}{x}

e 

\displaystyle sen(\theta )=\frac{x}{3}\Rightarrow \theta=arcsen\bigg (\frac{x}{3}\bigg ),

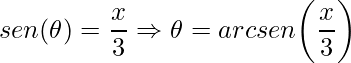ao substituir obtemos a resposta desejada 

\displaystyle \int\frac{\sqrt{9-x^{2}}}{x^{2}}dx=-\frac{\sqrt{9-x^{2}}}{x}-arcsen\bigg (\frac{x}{3}\bigg )+C.

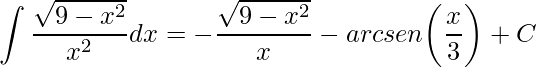Os exemplos dos tipos 2 e 3 serão apresentados nos próximos post. Caso já queira ir resolvendo eles serão os seguintes: 

2)\displaystyle \int\sqrt{x^{2}+4}dx

3)\displaystyle \int\frac{1}{x^{3}\sqrt{x^{2}-9}}dx