Propriedades dos Limites

Neste post apresentam-se as principais Propriedades dos Limites, porém sem fazer sua demostração. Estas propriedades são muito úteis na resolução de problemas envolvendo cálculo de limites.

1) Propriedade da unicidade do Limite:

Se $\lim\limits_{x\rightarrow a} f(x) = L$ e $\lim\limits_{x\rightarrow a} f(x) = M$ então $L = M$ .

2) Propriedade do Limite de uma função constante:

Se $f(x) = K$ para todo $x$ real, então para qualquer $a$ real, tem-se:

$\lim\limits_{x\rightarrow a} f(x) = \lim\limits_{x\rightarrow a} k = k$ .

Clique aqui para ver a Demonstração.

3) Propriedade da soma ou da subtração dos Limites:

Se $\lim\limits_{x\rightarrow a} f(x) = L$ e $\lim\limits_{x\rightarrow a} g(x) = M$ então:

$\lim\limits_{x\rightarrow a} (f(x) \pm g(x)) = \lim\limits_{x\rightarrow a} f(x) \pm \lim\limits_{x\rightarrow a} g(x) =L\pm M$ .

Clique aqui para ver a Demonstração.

4) Propriedade da multiplicação por escalar do Limite:

Para qualquer constante $K$ e $\lim\limits_{x\rightarrow a} f(x) = L$ :

$\lim\limits_{x\rightarrow a} (k \times f(x)) = k \times \lim\limits_{x\rightarrow a} f(x) = k \times L$ .

Obs: O sinal, $\times$ , simboliza simplesmente uma multiplicação entre dois termos e não o operador rotacional.

5) Propriedade da multiplicação de Limites:

Se $\lim\limits_{x\rightarrow a} f(x) = L$ e $\lim\limits_{x\rightarrow a} g(x) = M$ então:

$\lim\limits_{x\rightarrow a} (f(x) \times g(x)) = \lim\limits_{x\rightarrow a} f(x) \times \lim\limits_{x\rightarrow a} g(x) = L \times M$ .

Clique aqui para ver a Demonstração.

6) Propriedade da divisão de Limites:

Se $\lim\limits_{x\rightarrow a} f(x) = L$ , $\lim\limits_{x\rightarrow a} g(x) = M$ e $M\neq0$ então:

$\displaystyle \lim\limits_{x\rightarrow a} \frac{f(x)}{g(x)} = \frac{\lim\limits_{x\rightarrow a} f(x)}{\lim\limits_{x\rightarrow a} g(x)} = \frac{L}{M}$ .

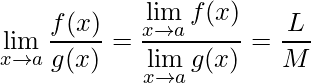Clique aqui para ver a Demonstração.

7) Propriedade da potência de Limites:

Se $\lim\limits_{x\rightarrow a} f(x) = L$ então:

$\displaystyle \lim\limits_{x\rightarrow a} (f(x))^{n} = (\lim\limits_{x\rightarrow a} f(x))^{n} = L^{n}$ .

8) Propriedade do exponencial do Limite:

Se $\lim\limits_{x\rightarrow a} f(x) = L$ e $b$ $\in$ $\mathbb{R}$ então:

$\displaystyle \lim\limits_{x\rightarrow a} b^{f(x)} = b^{\lim\limits_{x\rightarrow a} f(x)} = b^{L}$ .

9) Propriedade do logaritmo do Limite:

Se $\lim\limits_{x\rightarrow a} f(x) = L$ , $L>0$ , $b$ $\in$ $\mathbb{R}$ , $b>0$ , $b\neq1$ e $n\in\mathbb{N}$ então:

$\displaystyle \lim\limits_{x\rightarrow a} (log_{b}f(x)) = log_{b}(\lim\limits_{x\rightarrow a} f(x)) = log_{b}L$ .

10) Propriedade da raiz do Limite:

Se $\lim\limits_{x\rightarrow a} f(x) = L$ , $n\in\mathbb{N}$ e $L>0$ quando $n$ for par então:

$\displaystyle \lim\limits_{x\rightarrow a} \sqrt[n]{f(x)} = \sqrt[n]{\lim\limits_{x\rightarrow a} f(x)} = \sqrt[n]{L}$ .

11) Propriedade do confronto ( sanduíche ) dos Limites:

Se $\lim\limits_{x\rightarrow a}h(x)=\lim\limits_{x\rightarrow a}g(x)=L$ tal que $h(x)\leq f(x)\leq g(x)$ então:

$\lim\limits_{x\rightarrow a} f(x) = L$ .

12) Propriedade dos polinômios:

Esta propriedade é uma combinação das propriedades 3 e 4. Seja $p(x)=b_{n}x^{n}+b_{n-1}x^{n-1}+\cdots+b_{1}x+b_{0}$ um polinômio qualquer, onde os $b_{n}$ são constantes arbitrárias, tem-se:

$\lim\limits_{x\rightarrow a} p(x) = \lim\limits_{x\rightarrow a}(b_{n}x^{n}+b_{n-1}x^{n-1}+\cdots+b_{1}x+b_{0}) =$

$= \lim\limits_{x\rightarrow a}b_{n}x^{n}+\lim\limits_{x\rightarrow a}b_{n-1}x^{n-1}+\cdots+\lim\limits_{x\rightarrow a}b_{1}x+\lim\limits_{x\rightarrow a}b_{0} =$

$= b_{n} \lim\limits_{x\rightarrow a}x^{n}+b_{n-1} \lim\limits_{x\rightarrow a}x^{n-1}+\cdots+b_{1} \lim\limits_{x\rightarrow a}x+b_{0} \lim\limits_{x\rightarrow a} =$

$= p(a)$ .

Logo, $\lim\limits_{x\rightarrow a}p(x) = p(a)$ .

13) Propriedade da divisão de polinômios:

Nos limites da forma 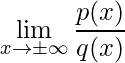$\displaystyle \lim\limits_{x\rightarrow \pm\infty}\frac{p(x)}{q(x)}$ em que $p(x)$ e $q(x)$ são polinômios em $x$ , prevalecem os termos de maior grau de ambos os polinômios quando for calcular o limite, ou seja, se

$p(x)=a_{m}x^{m}+a_{m-1}x^{m-1}+\cdots+a_{1}x+a_{0}$
$q(x)=b_{n}x^{n}+b_{n-1}x^{n-1}+\cdots+b_{1}x+b_{0}$

então

$\displaystyle \lim\limits_{x\rightarrow \pm\infty}\frac{p(x)}{q(x)}=\lim\limits_{x\rightarrow \pm\infty}\frac{a_{m}x^{m}}{b_{n}x^{n}}$ .

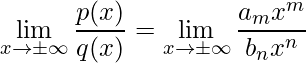Continue seus estudos acompanhando os Exemplos iniciais de limites.

Propriedades dos Limites

Propriedades dos Limites

1) Propriedade da unicidade do Limite:

2) Propriedade do Limite de uma função constante:

3) Propriedade da soma ou da subtração dos Limites:

4) Propriedade da multiplicação por escalar do Limite:

5) Propriedade da multiplicação de Limites:

6) Propriedade da divisão de Limites:

7) Propriedade da potência de Limites:

8) Propriedade do exponencial do Limite:

9) Propriedade do logaritmo do Limite:

10) Propriedade da raiz do Limite:

11) Propriedade do confronto ( sanduíche ) dos Limites:

12) Propriedade dos polinômios:

13) Propriedade da divisão de polinômios:

Damos valor à sua privacidade

Cookies estritamente necessários

Cookies de desempenho

Cookies de funcionalidade

Cookies de publicidade

Propriedades dos Limites

1) Propriedade da unicidade do Limite:

2) Propriedade do Limite de uma função constante:

3) Propriedade da soma ou da subtração dos Limites:

4) Propriedade da multiplicação por escalar do Limite:

5) Propriedade da multiplicação de Limites:

6) Propriedade da divisão de Limites:

7) Propriedade da potência de Limites:

8) Propriedade do exponencial do Limite:

9) Propriedade do logaritmo do Limite:

10) Propriedade da raiz do Limite:

11) Propriedade do confronto ( sanduíche ) dos Limites:

12) Propriedade dos polinômios:

13) Propriedade da divisão de polinômios:

Damos valor à sua privacidade

Cookies estritamente necessários

Cookies de desempenho

Cookies de funcionalidade

Cookies de publicidade

Faça aulas personalizadas sobre conteúdos específicos de Matemática e Raciocínio Lógico