Derivando uma função implícita – diferenciação implícita
Na maioria dos post até aqui resolvemos casos em que a função estava escrita de forma explícita, entretanto quando estamos Derivando uma função implícita temos que ter uma série de outros cuidados. Assim, este post será dedicado para este fim, mas para iniciar devemos ter claro a diferença entre estas duas formas.
Uma função está escrita na forma explícita quando a variável y=f(x) está de uma lado da igualdade e do outro lado os termos em x, veja exemplos,
![]() ou ainda
ou ainda 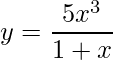 .
.
Caso contrário, a função está escrita na forma implícita, sendo que algumas vezes é impossível isolarmos a variável dependente y=f(x)
![]() ou simplesmente
ou simplesmente ![]() .
.
Exercícios resolvidos
Derive implicitamente as seguintes funções:
1)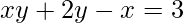
Este primeiro exercício trouxemos uma função implícita, mas que facilmente podemos transforma em explícita. Isto porque a nossa ideia neste exercício é comparar o resultado fim ao derivar pelas duas formas. Assim iniciamos derivando implicitamente.Como queremos saber a derivada desta função, o primeiro passo é derivar os dois lados da igualdade, conforme já fazíamos com as funções explícitas
![Rendered by QuickLaTeX.com \displaystyle \frac{d}{dx}\big[xy+2y-x\big ]=\frac{d}{dx}\big[3\big ]](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-66e417866abcba25346334d8ee535de6_l3.png) ,
,
usando as propriedade das derivadas podemos abrir esta expressão na soma de “pequenas” derivadas
![Rendered by QuickLaTeX.com \displaystyle \frac{d}{dx}\big[xy\big ]+\frac{d}{dx}\big[2y\big ]-\frac{d}{dx}\big[x\big ]=\frac{d}{dx}\big[3\big ]](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-2a32233c5ddf370211e1c791967a01fa_l3.png) .
.
Observe que não sabemos quem é a função y, mas tratamos ela como uma função diferenciável em x, assim temos no primeiro termo a derivada do produto e os demais são derivadas diretas
![Rendered by QuickLaTeX.com \displaystyle \frac{d}{dx}\big[x\big ]\cdot y+x\cdot\frac{d}{dx}\big[y\big ]+2\frac{dy}{dx}-1=0](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-6a0fbf22f6f90bdd5c533c25a86170f6_l3.png) ,
,
que resulta em
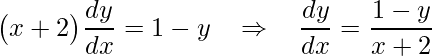 .
.
Até aqui já temos a derivada desejada, mas para fins de comparação devemos tomar a expressão dada no enunciado e isolarmos y, obtendo assim a forma explícita. Em seguida, substituir y na derivada encontra
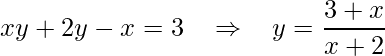
substituindo encontraremos
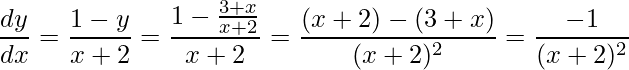 .
.
Agora para comparar basta derivar a função 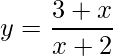 , usando Derivada da divisão
, usando Derivada da divisão
![Rendered by QuickLaTeX.com \displaystyle \frac{dy}{dx}=\frac{\frac{d}{dx}[3+x]\cdot (x+2)-\frac{d}{dx}[x+2]\cdot(3+x)}{(x+2)^{2}}=\frac{-1}{(x+2)^{2}}](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-aa6e94be3bf014d5e87ec670b0dbbce1_l3.png) ,
,
observe que os resultados são iguais, mas nem sempre conseguimos transformar uma função implícita em explícita, como o exemplo a seguir.
2)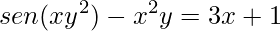
Como descrevemos no exercício anterior, o primeiro passo é derivar ambos os lados da igualdade
![Rendered by QuickLaTeX.com \displaystyle \frac{d}{dx}\big[sen(xy^{2})-x^{2}y\big]=\frac{d}{dx}\big[3x+1\big]](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-7b4f3397ec9e1423fb151acf0b57ba80_l3.png) ,
,
em seguida, aplicar a propriedade da derivada da soma/subtração
![Rendered by QuickLaTeX.com \displaystyle \frac{d}{dx}\big[sen(xy^{2})\big]-\frac{d}{dx}\big[x^{2}y\big]=\frac{d}{dx}\big[3x\big]+\frac{d}{dx}\big[1\big]](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-470733dba3f254af178601c55dfcbf55_l3.png) .
.
Agora resolveremos cada um dos termos separadamente, depois de obter a derivada de cada termo, substituiremos para então obter a solução desejada. No primeiro termo temos que derivar uma função seno, assim aplicaremos a regra da cadeia, onde usaremos ![]() assim
assim
![Rendered by QuickLaTeX.com \displaystyle\frac{d}{dx}\big[sen(xy^{2})\big]=\frac{d}{du}\big[sen(u)\big]\cdot \frac{d}{dx}\big[xy^{2}\big]](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-7e6f91ec6b1df768b0970f401fc5d4a9_l3.png) .
.
Agora observe que na derivada de x temos um produto, logo devemos aplicar a derivada do produto onde teremos
![Rendered by QuickLaTeX.com \displaystyle \frac{d}{du}\big[sen(u)\big]\cdot \frac{d}{dx}\big[xy^{2}\big]=cos(u)\cdot\bigg(\frac{d}{dx}\big[x\big]y^{2}+x\frac{d}{dx}\big[y^{2}\big]\bigg)=](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-76abdf14c179e241f4727c89a25f2fef_l3.png)
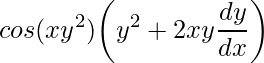 .
.
No segundo termo a ser derivado devemos aplicar novamente a derivada do produto
![Rendered by QuickLaTeX.com \displaystyle \frac{d}{dx}\big[x^{2}y\big]=\frac{d}{dx}\big[x^{2}\big]y+x^{2}\frac{d}{dx}\big[y\big]=2xy+x^{2}\frac{dy}{dx}](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-4dc2a383d1bfeefc229e594a7599f510_l3.png) .
.
Nos demais termos devemos aplicar a derivada direta, apenas utilizando as derivadas das funções básicas
![Rendered by QuickLaTeX.com \displaystyle \frac{d}{dx}\big[3x\big]=3](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-055a74c8c2c14ca7ec8beeebf1f6fcb6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \frac{d}{dx}\big[1\big]=0](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-9fedb5c518f03664c15a17b8f63b0041_l3.png) .
.
Obtida todas as derivadas, voltamos e substituímos cada um dos resultados nos seus respectivos lugares
![Rendered by QuickLaTeX.com \displaystyle \frac{d}{dx}\big[sen(xy^{2})\big]-\frac{d}{dx}\big[x^{2}y\big]=\frac{d}{dx}\big[3x\big]+\frac{d}{dx}\big[1\big]\: \: \: \Rightarrow](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-60b6cbed4401792dc71fa3fc0a4dfd12_l3.png)
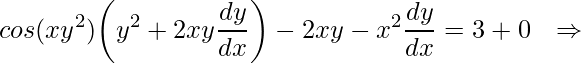
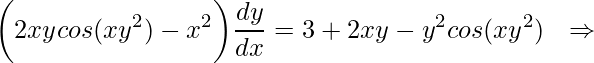
 .
.
Acompanhe também explicações e resoluções de outros exemplos em vídeo, clicando aqui.



Deixe um comentário