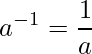Por que qualquer número elevado a zero é igual a 1?

Um dos resultados mais curiosos e frequentemente questionados pelos alunos ao estudar funções exponenciais é o valor de uma potência com expoente zero. Afinal, se elevar um número a uma potência significa multiplicá-lo várias vezes, como pode ser que “nenhuma multiplicação” resulte em $1$ ?

Neste post, vamos apresentar uma explicação intuitiva e consistente com as regras da matemática para entender por que qualquer número elevado a zero é igual a $1$ . Essa ideia não surge por acaso — ela é uma consequência natural das propriedades das potências. Vamos analisar o comportamento da função exponencial e observar um padrão que justifica essa definição.

Explicação intuitiva:

Dado um número qualquer $a$ , temos que

$a^0=a^{1-1}$

Sabemos que:

$a^1=a$
$a^{-1}=\frac{1}{a}$
$a^{1-1}=a^1 \times a^{-1}$

Logo temos que

$a^0=a^{1-1} = a \times \frac{1}{a} = \frac{a}{a} = 1$

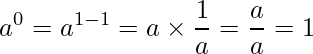
Por que qualquer número elevado a zero é igual a 1?

A razão pela qual qualquer número real (exceto zero) elevado a zero é igual a 1 tem base em regras fundamentais da aritmética de potências e na coerência matemática. Nesse sentido, vamos entender isso passo a passo, de maneira lógica e acessível.

1. Regra das potências com mesma base

Primeiramente, considere uma das propriedades mais importantes das potências:

$a^m \div a^n = a^{m - n}$

Essa regra é válida para qualquer número real $a \neq 0$ e quaisquer expoentes $m$ e $n$ . Agora, se considerarmos o caso em que $m = n$ , temos:

$a^m \div a^m = a^{m - m} = a^0$

Por outro lado, sabemos que qualquer número (exceto o zero) dividido por ele mesmo é igual a 1. Portanto, isso implica diretamente que:

$a^m \div a^m = 1 \quad \Rightarrow \quad a^0 = 1$

2. Padrão observado ao diminuir o expoente

Vamos agora observar um padrão numérico usando a base 2, o que torna a ideia ainda mais intuitiva:

$\begin{align<em>} 2^3 &= 8 \ 2^2 &= 4 \ 2^1 &= 2 \ 2^0 &= ? \end{align</em>}$

Nesse caso, a cada vez que reduzimos o expoente em 1 unidade, o resultado é dividido por 2. Veja:

$8 \div 2 = 4,\quad 4 \div 2 = 2,\quad 2 \div 2 = 1$

Portanto, para manter a coerência dessa sequência, devemos concluir que:

$2^0 = 1$

Esse mesmo raciocínio vale para qualquer base positiva diferente de zero. Ou seja, o comportamento é geral.

3. Interpretação com função exponencial contínua

Além disso, podemos considerar a função exponencial $f(x) = a^x$ , que é amplamente usada em matemática e ciências aplicadas. Para que essa função seja contínua e bem comportada no ponto $x = 0$ , ela deve satisfazer o seguinte limite:

$\lim_{x \to 0} a^x = 1 \quad \text{(para } a > 0\text{)}$

Assim, a definição $a^0 = 1$ é coerente também com a continuidade da função, além de ser útil para manter propriedades fundamentais da matemática.

4. E quanto a 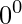$0^0$ ?

Agora, vale destacar uma exceção importante: a expressão $0^0$ . Em muitos contextos, como na análise matemática, ela é considerada indeterminada. Contudo, em outras áreas, como a combinatória e o desenvolvimento de séries de potências, define-se frequentemente $0^0 = 1$ por conveniência prática.

Em resumo, o valor de $0^0$ depende do contexto em que está sendo usado.

Conclusão

$\boxed{a^0 = 1 \quad \text{para todo } a \neq 0}$

Portanto, essa definição não apenas mantém a coerência das propriedades das potências, como também facilita o uso da matemática em diferentes contextos. Além disso, ela garante a continuidade das funções exponenciais e torna mais fácil o desenvolvimento de teorias algébricas e computacionais.

Referências

Wikipedia – Potência (matemática)
➤ https://pt.wikipedia.org/wiki/Potência_(matemática)
Âncora sugerida: “definição formal de potência na matemática”
Khan Academy – Propriedades das potências
➤ https://pt.khanacademy.org/math/algebra/x2f8bb11595b61c86:exponents
Âncora sugerida: “aulas gratuitas sobre expoentes”
Wolfram MathWorld – Exponentiation (em inglês)
➤ https://mathworld.wolfram.com/Exponentiation.html
Âncora sugerida: “tratamento formal da exponenciação”
https://www.dicasdecalculo.com.br/propriedades-das-potencias
https://www.dicasdecalculo.com.br/funcao-exponencial
https://www.dicasdecalculo.com.br/exercicios-potencias

Por que qualquer número elevado a zero é igual a 1?

Baixe de forma gratuita nossos Ebooks e treinamentos

Explicação intuitiva: