Aprenda o que são eventos aleatórios e como calcular suas probabilidades com exemplos práticos. Ideal para estudantes e concurseiros.
Você já se perguntou qual a chance de tirar “cara” ao lançar uma moeda? Ou de acertar os 6 números da Mega-Sena? Esses são exemplos clássicos da probabilidade de eventos aleatórios, um tema muito cobrado em provas do ENEM, concursos públicos e vestibulares.
👉 Por esse motivo, dominar esse assunto é essencial para quem deseja se destacar nas avaliações.
Neste post, você vai aprender o que são eventos aleatórios, como calcular a probabilidade de ocorrência, e ainda verá exemplos práticos explicados passo a passo.
📘 O que é um Evento Aleatório?
Antes de tudo, é importante entender o que significa “evento aleatório”. Trata-se de qualquer resultado de um experimento cujo desfecho não pode ser previsto com certeza.
Por exemplo, ao lançar um dado, não sabemos exatamente qual número sairá. Além disso, ao sortear uma carta de um baralho, não temos como saber de antemão o naipe. Ou seja, o elemento de incerteza é sempre presente.
Por exemplo:
- Ao lançar um dado, não sabemos qual número sairá.
- Ao tirar uma carta de um baralho, não há como prever o naipe.
- Ao escolher alguém de uma turma, não podemos afirmar se essa pessoa é canhota.
👉 Em todos esses casos, o resultado depende do acaso.
🧮 Como calcular a probabilidade de eventos aleatórios?
A fórmula clássica para calcular a probabilidade de um evento 
ocorrer é:
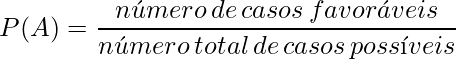
onde:
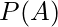é a probabilidade do evento acontecer;- casos favoráveis: situações que satisfazem o evento;
- casos possíveis: todas as situações igualmente prováveis.
🎯 1º Exemplos resolvido
Exemplo 1:
Qual a probabilidade de, ao lançar um dado de 6 faces, sair o número 3?
Solução:
- Casos favoráveis: 1 (apenas o número 3)
- Casos possíveis: 6 ( 1, 2, 3, 4, 5, 6 todos os casos)
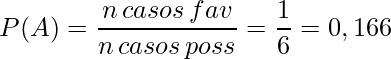
Ou seja, a probabilidade de sair o número 3 no lançamento de um dado é de 16% (basta multiplicar o resultado por 100 para ter a porcentagem exata)
Assim, se quiser praticar mais, a Khan Academy oferece exercícios interativos gratuitos sobre esse tema https://pt.khanacademy.org/math/statistics-probability/probability-library
🎯 2º Exemplos resolvido
Exemplo 1:
Qual a probabilidade de, ao lançar um dado de 6 faces, sair um número par?
Solução:
- Casos favoráveis: 3 (2, 4, 6 números pares favoráveis)
- Casos possíveis: 6 ( 1, 2, 3, 4, 5, 6 todos os casos)
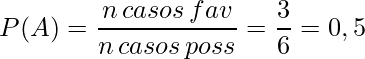
Ou seja, a probabilidade de sair um número par no lançamento de um dado é de 50%
🎯 Exercício para o leitor
Em uma caixa há 2 livros de história, 6 de matemática e 4 de português. Se retirarmos um livro dessa caixa, ao acaso, qual a probabilidade dele ser:
a) um livro de história?
b) um livro de matemática?
d) um livro de português?
(respostas no final do post)
🔄 Tipos de eventos aleatórios
Até aqui, vimos como calcular probabilidades simples.
A seguir, vamos conhecer os principais tipos de eventos aleatórios:
- Eventos mutuamente exclusivos: não podem ocorrer ao mesmo tempo (ex: cara ou coroa).
- Eventos independentes: um resultado não interfere no outro (ex: jogar dois dados).
- Eventos complementares: a soma de suas probabilidades é igual a 1 (ex: sair par ou não sair par).
👉 Sendo assim, conhecer essas classificações ajuda bastante na hora de resolver exercícios mais complexos.
De forma mais técnica, um evento aleatório pode ser entendido como qualquer subconjunto do espaço amostral https://pt.wikipedia.org/wiki/Evento_aleat%C3%B3rio.
💡 Dica final para provas
Antes de resolver qualquer questão, verifique se todos os resultados são equiprováveis.
⚠️ Caso contrário, aplicar a fórmula diretamente pode levar ao erro.
Por isso, cuidado com a linguagem do enunciado. Muitas vezes, ele apresenta armadilhas que confundem o estudante.
📝 Conclusão com transições
Em resumo, a probabilidade de eventos aleatórios é um conteúdo essencial para estudantes e concurseiros.
Compreender esse tema te permite resolver problemas com mais segurança, lógica e clareza.
👉 Agora é com você!
Pratique com os exemplos vistos aqui e desafie-se com novos exercícios.
Por fim, se quiser se aprofundar ainda mais, baixe nosso material completo de raciocínio lógico clicando aqui.
Respostas do exercício: a) 
, b)
, c) 
