Cálculo da Área de superfícies de revolução – “cascas” de objetos
A Área de superfícies de revolução são aquelas geradas ao girar uma curva em torno de um eixo. Por exemplo, se temos uma curva f(x) de 
e girarmos a curva em torno do eixo x teremos a “casca” de um objeto, ou seja, a superfície de revolução.
Definição de área de superfícies de revolução
Seja f(x) uma curva suave e não negativa definida em . Assim, ao girar esta curva em torno de um eixo x obteremos uma superfície de revolução. Conforme figura a seguir:
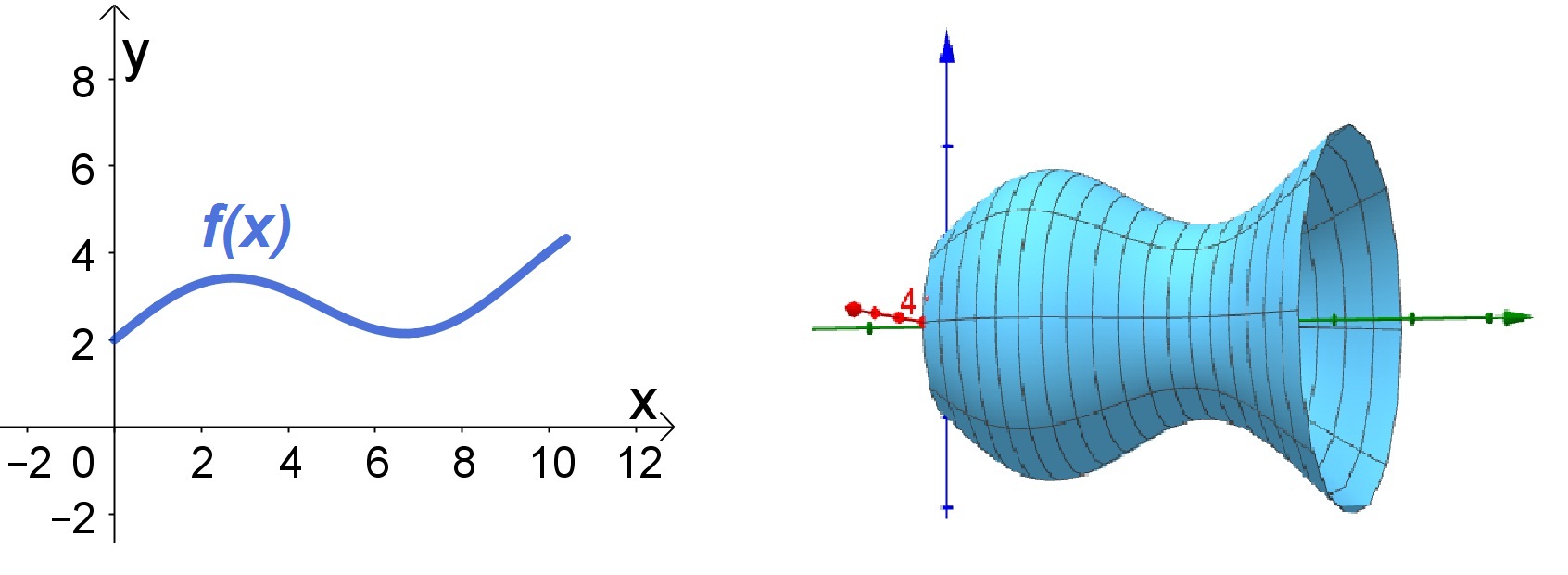
Calculo da Área de superfícies de revolução
Em resumo: a ideia geral para a dedução da fórmula da área da superfície de revolução é fatiar em secções em troncos de cone, e em seguida, fazer a espessura tender a zero.
Inicialmente, devemos dividir em a área em troncos de cones em 
, ao traçarmos retas entre dois pontos.
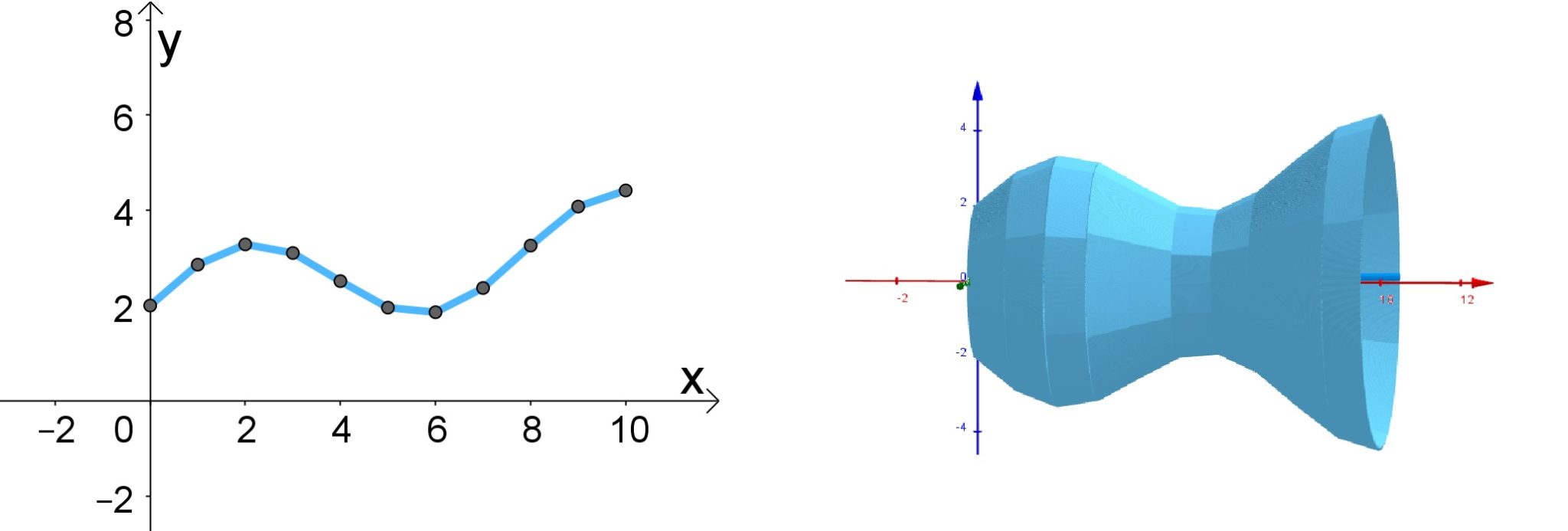
Da geometria espacial sabemos que a área lateral dos troncos de cones é
onde 
são os raios e 
a altura do tronco de cone.
Em seguida, devemos somando os n intervalos, onde teremos uma aproximação da Área de superfícies de revolução
.
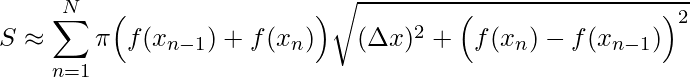Além disso, pelo Teorema do Valor Médio
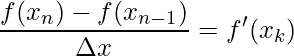
para 
e pelo Teorema do Valor Intermediário
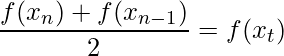
para 
, temos
.
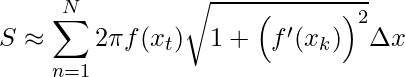Por fim, ao tomarmos o limite de 
tendendo a zero teremos a construção da integral
.
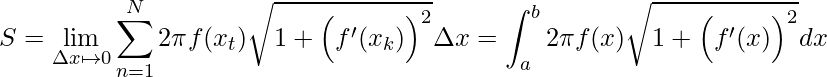De forma análoga, podemos construir a fórmula para o caso de girarmos entorno do eixo y.
Veja um exemplo resolvido clincando aqui.
