aplicações >

Cálculo da área de superfícies de revolução

Cálculo da área de superfícies de revolução – aplicações das integrais definidas

Neste post apresentaremos a resolução do Cálculo da área de superfícies de revolução. Lembrando que já publicamos de forma resumida a construção da fórmula em que calcula a área de superfícies de revolução, também chamada de casca de um objeto. Assim, nos dedicaremos hoje apenas na sua aplicação.  

Primeiramente recorde que a fórmula é dada por 

\displaystyle S= \int_{a}^{b}2\pi f(x)\sqrt{1+\Big({f}'(x)\Big)^{2}}dx

ao girarmos f(x) entorno do eixo x.

Determine a área da casca do objeto gerado ao girarmos a função f(x) entorno do eixo dado.

1)\displaystyle f(x)=\sqrt{4-x^{2}} entorno do eixo x com \displaystyle -1\leq x\leq 1

Na aplicação da fórmula devemos saber qual é a derivada de f(x), para isto aplicaremos a Regra da Cadeia, pois se trata de uma função composta.  

Dessa forma, temos 

\displaystyle f'(x)=\frac{d}{du}\big[\sqrt{u}\big]\cdot \frac{d}{dx}\big[4-x^{2}\big]=-\frac{x}{\sqrt{4-x^{2}}}.

Agora que temos todos os elementos podemos aplicar a fórmula

\displaystyle S= \int_{-1}^{1}2\pi \sqrt{4-x^{2}}\sqrt{1+\frac{x^{2}}{4-x^{2}}}dx.

Observe que podemos fazer algumas simplificações a partir do minimo múltiplo comum no segundo termo raiz 

\displaystyle S=\int_{-1}^{1}2\pi \sqrt{4-x^{2}}\sqrt{\frac{4-x^{2}+x^{2}}{4-x^{2}}}dx=

\displaystyle \int_{-1}^{1}2\pi \sqrt{4-x^{2}}\sqrt{\frac{4}{4-x^{2}}}dx=

\displaystyle \int_{-1}^{1}2\pi \sqrt{4-x^{2}}\frac{2}{\sqrt{4-x^{2}}}dx=.

Sobrando assim uma integral simples

\displaystyle S=\int_{-1}^{1}4\pi dx.

Resolvendo a integral obteremos o valor desejado

\displaystyle S=4\pi x\bigg|_{-1}^{1}=8\pi.

Na figura a seguir temos a representação da área encontrada.

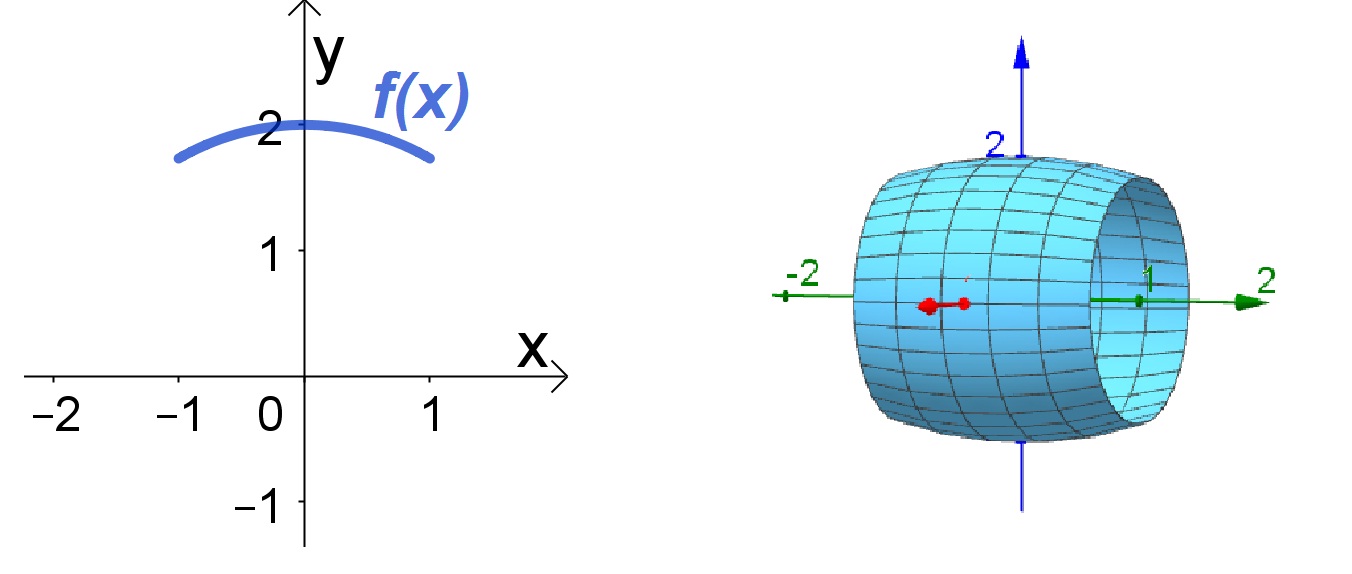
Cálculo da área de superfícies de revolução

Caso surgiu alguma dúvida, deixe ela nos comentários a seguir que buscaremos esclarecer.

Publicado em 15/09/2018, em aplicações, Integrais.