Cálculo da área entre curvas

Possivelmente o Cálculo da área entre curvas seja a aplicação mais comum das integrais. Esta aplicação decorre da própria ideia de integral, que é a área de uma região plana sob uma curva. Assim, partiremos do conceito de integral como área e expandiremos para área entre curvas.

Área sob uma curva

Seja A a região de um plano delimitada pela curva contínua f(x), o eixo das abscissas (y=0) e as retas verticais x = a e x = b. 

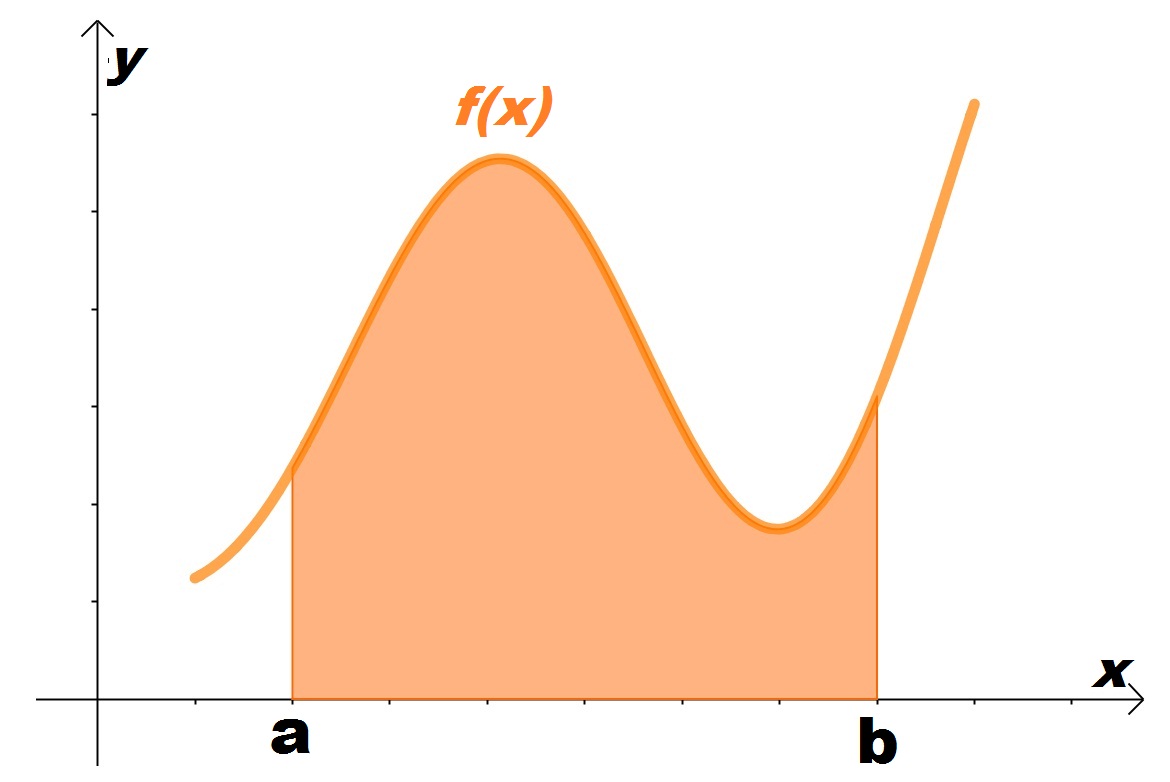
Como já vimos no post passado, esta área A é dada pela integral

. 

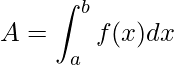Calculo da área entre curvas

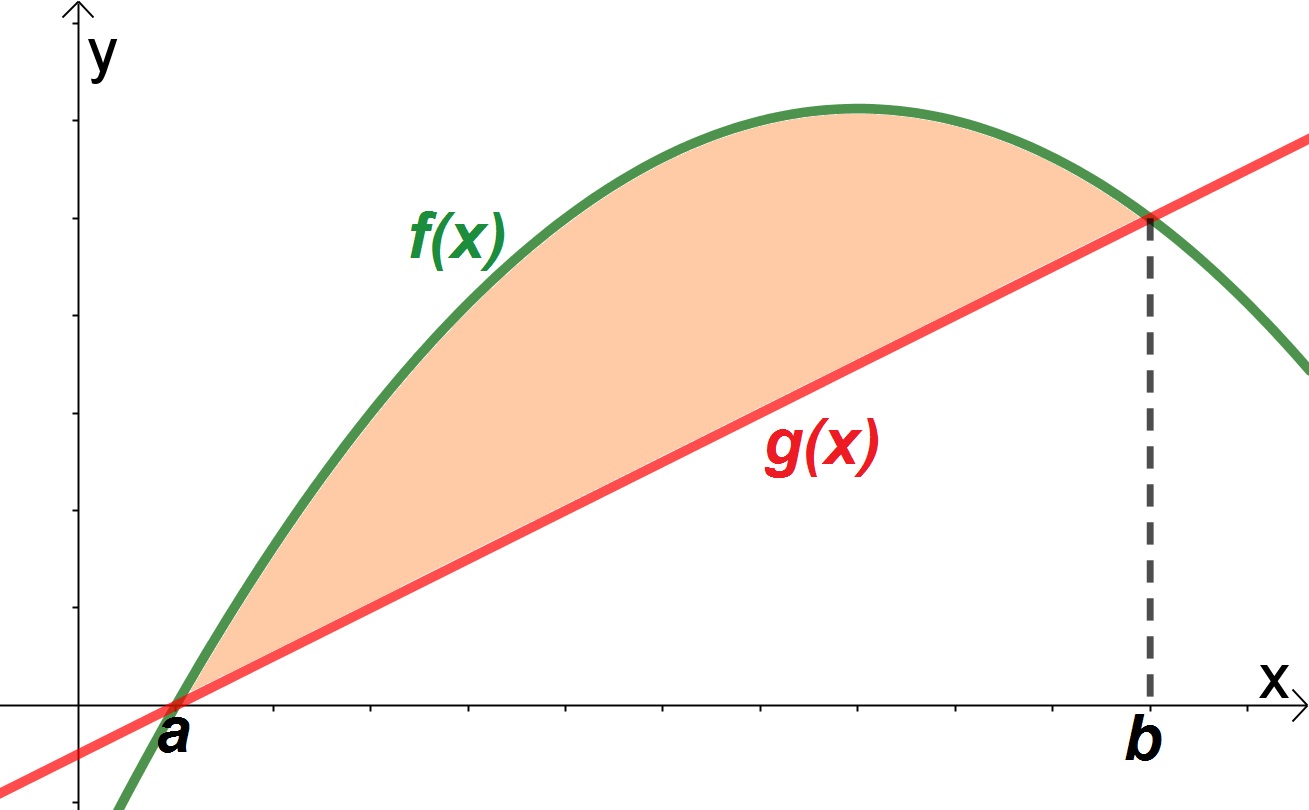
Seguindo a mesma lógica da área sob uma curva, podemos construir a fórmula para calcular a área entre curvas. Assim, definimos duas curvas continuas f(x) e g(x), onde f(x) seja maior ou igual de g(x) em todo intervalo [a,b]. Ao calcular a área sob cada uma das curvas temos 

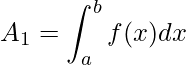
e

.

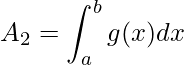Observe nos gráficos a seguir estas duas áreas.

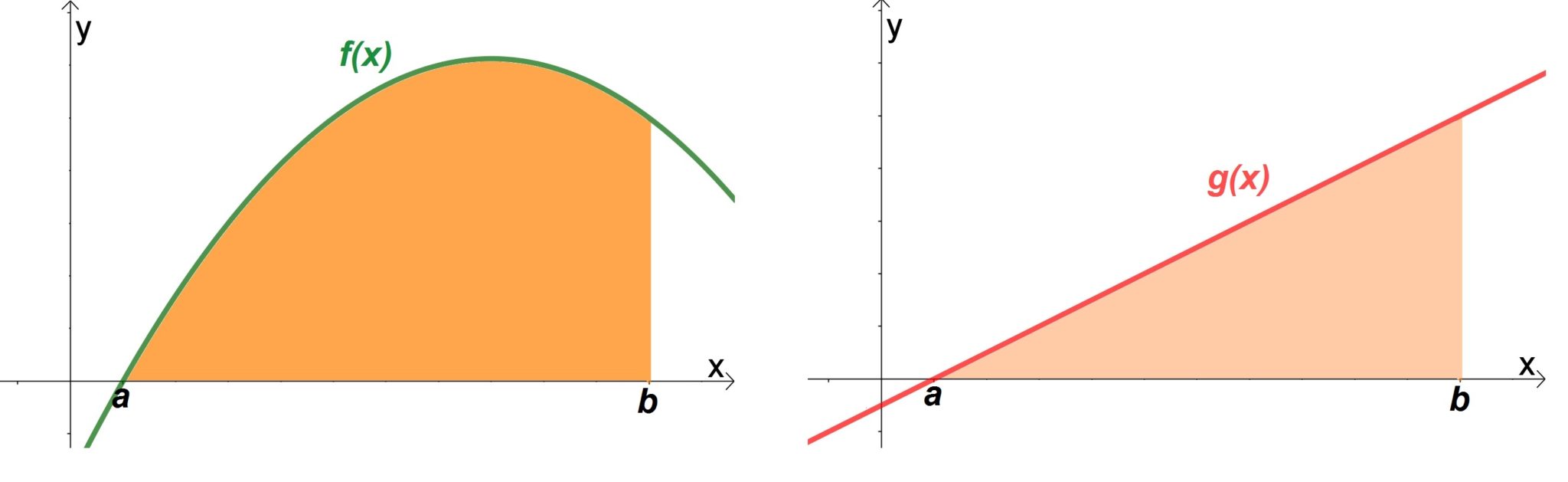
Assim, se queremos calcular a área entre a curva f(x) e a curva g(x), devemos subtrair de a área . Dessa forma, temos

.

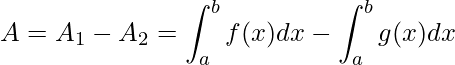Conforme as propriedades das integrais, a subtração de integrais definidas no mesmo intervalo é igual a integral da subtração, assim

.

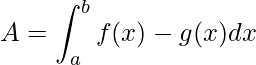Exemplo:

Calcule a área entre as curvas 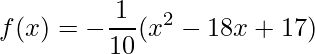 e .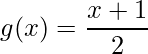

O primeiro passo é encontrar os pontos de intersecção e avaliar onde f(x) é maior do que g(x) e vice-versa. Desse modo, os pontos de intersecção são onde f(x)=g(x). Logo, 

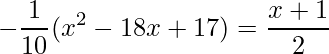
assim,

.

Desse modo, ao encontrar as raízes obtemos x=2 e x=11. Assim, concluímos que a região desejada fica entre estes dois valores de x. Em seguida, devemos identificar qual das funções é maior neste intervalo. Para isto avaliamos as duas funções em um ponto qualquer entre x=2 e x=11. Assim,

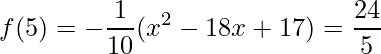
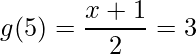
Portanto, no intervalo indicado f(x) é maior do que g(x). Assim sendo, devemos apenas aplicar a integral

.

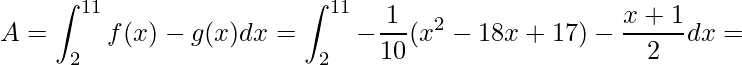
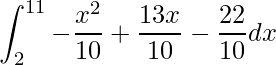Resolvendo a integral,

.

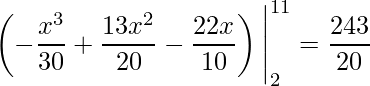Algumas observações:

1. Não é necessário que f(a)=g(a) e f(b)=g(b) sejam iguais.
2. Caso f(x) não seja maior que g(x) em todo intervalo de integração, devemos separar os intervalos.
3. A área desejada pode estar entre mais do que duas curvas, assim devemos analisar os pontos de intersecção. Veja exemplo a seguir:

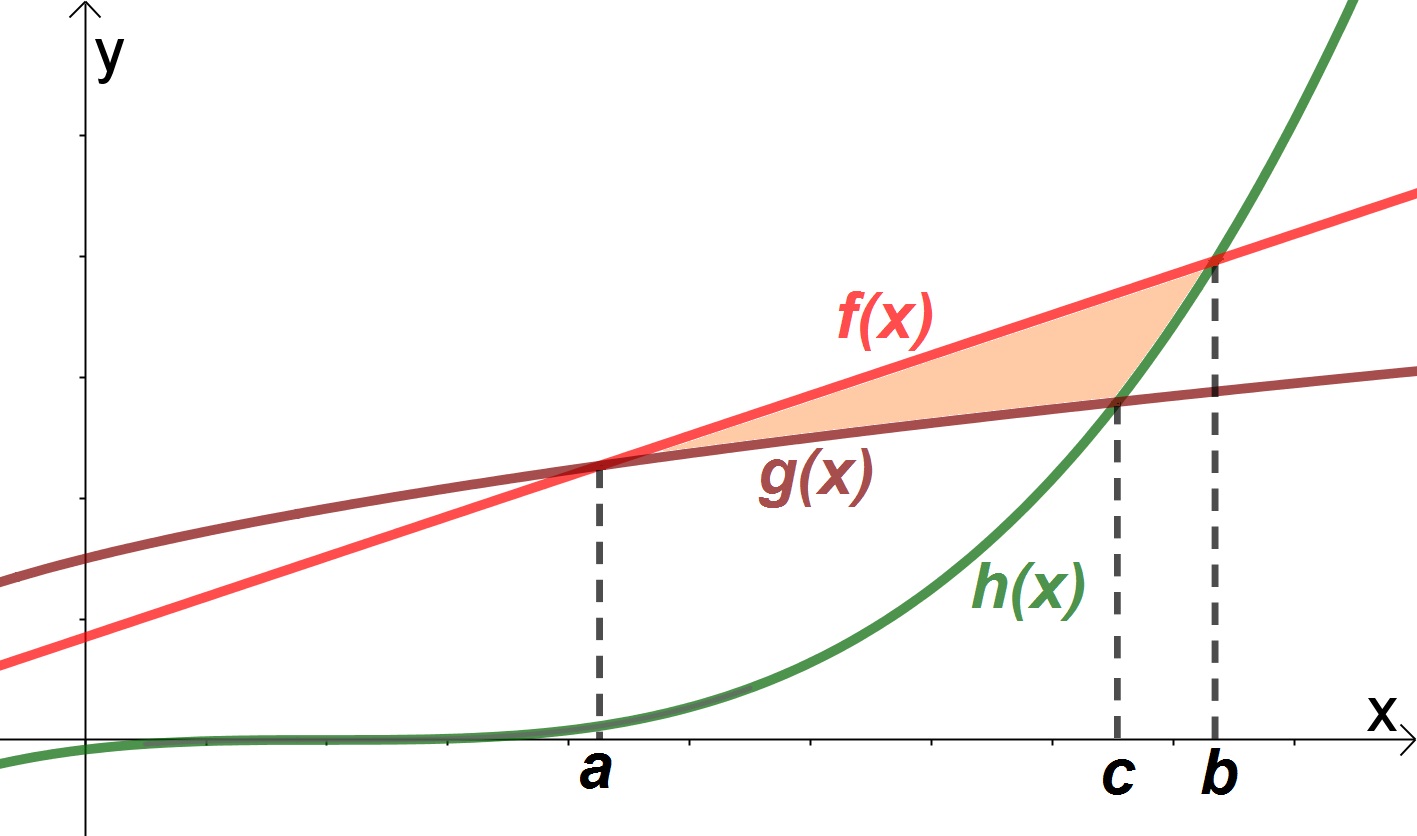
A área entre as curvas f(x), g(x) e h(x) é dada por

.

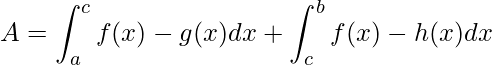Nos próximos post estaremos resolvendo exercícios envolvendo cálculo de áreas.