Integração por Substituição: a antiderivada da Regra da cadeia
No post anterior apresentamos a integral como a busca da família das antiderivadas de uma função. Neste sentido apresentaremos hoje o Método da Integração por Substituição que pode ser apresentado como a antidiferenciação da Regra da Cadeia.
Como motivação, observemos a seguinte integral e perceba que nesta não podemos aplicar as fórmulas das integrais imediadas
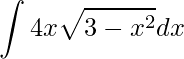 .
.
Assim precisamos aplicar alguma metodologia que transforme a integral dada por outra em que conhecemos sua integral imediata. Uma maneira de integral é utilizar o Método da Integração por Substituição, que como o próprio nome diz, devemos aplicar uma substituição.
Entretanto, antes de aplicar o método, vamos mostrar porque a Integração por Substituição é a presentada como a antidiferenciação da Regra da Cadeia. Lembre-se que a Regra da Cadeia é dada por
![Rendered by QuickLaTeX.com \displaystyle \frac{d}{dx}\bigg[f\big(g(x)\big)\bigg]=f'\big(g(x)\big)g'(x)](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-52f8f9f5957edf99c19b3a8192c12f69_l3.png) ,
,
aplicando a integral em ambos os lados temos
![Rendered by QuickLaTeX.com \displaystyle \int \frac{d}{dx}\bigg[f\big(g(x)\big)\bigg]dx=\int f'\big(g(x)\big)g'(x)dx](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-4d3c44f8a2a460baa005d37ef93b2fe6_l3.png)
Tomando ![]() , derivando temos
, derivando temos 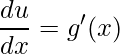 e multiplicando ambos os lados por
e multiplicando ambos os lados por ![]() temos
temos ![]() . Assim substituindo na expressão anterior temos
. Assim substituindo na expressão anterior temos
![Rendered by QuickLaTeX.com \displaystyle \int \frac{d}{dx}\bigg[f\big(g(x)\big)\bigg]dx=\int f'\big(g(x)\big)g'(x)dx=](https://www.dicasdecalculo.com.br/wp-content/ql-cache/quicklatex.com-3302669d3ae52ac2de0b158558094263_l3.png)
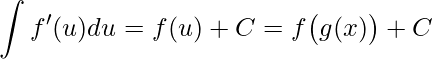 .
.
Deste modo obtemos a família da função composta original, antes de ser aplicada a Regra da Cadeia.
Agora voltamos a integral dada na motivação deste post e aplicaremos a Integração por Substituição
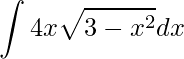 .
.
Substituindo ![]() e derivando
e derivando  temos agora uma integral na variável u
temos agora uma integral na variável u
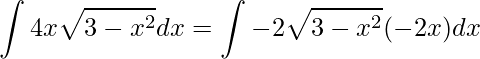
substituindo teremos
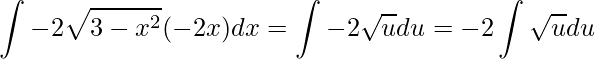 .
.
Em seguida, aplicando a integral imediata da potência
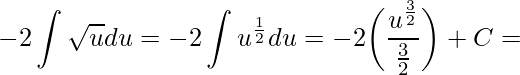
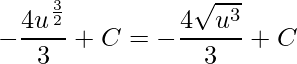 .
.
Por fim, substituindo ![]() obteremos o valor da integral indefinida
obteremos o valor da integral indefinida
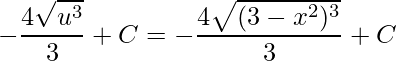 .
.
Logo,
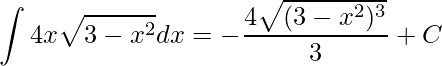 .
.
Caso queira fazer uma “prova” para verificar o resultado encontrado, basta derivar e comparar com o integrando. Continue seus estudos acompanhando outros exemplos resolvidos clicando aqui.

