Integral Definida: Área sob uma Curva 

O nome Integral Definida vem do fato que a integral está restrita a um intervalo. Assim se temos uma função f(x) e aplicarmos a integral definida em [a,b] obteremos um valor que não depende mais de x. Este valor encontrado é a Área que está limitada entre a função f(x), o eixo x e as retas x=a e x=b, como na figura.

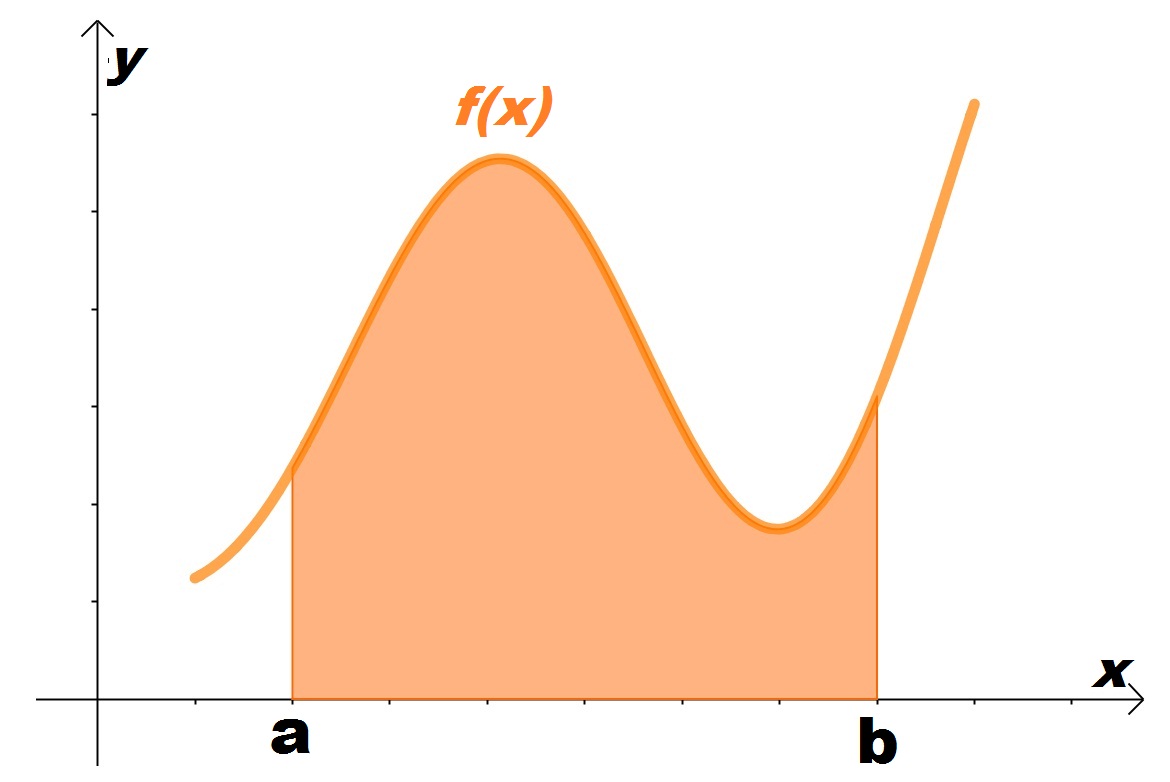
Definição: Se a função f(x) for contínua em [a,b], onde este intervalo seja dividido em n partes iguais de comprimento e tomarmos para cada i-ésimo intervalo um , i=1,…,n, a integral definida de f(x) em [a,b] é dada por 

,

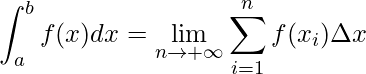se este limite existir.

Exemplo 1: encontre a área sob a função f(x)=sen(x) no intervalo  .

Observe que o exemplo nos pede que calculemos a área localizada entre a curva, o eixo e no intervalo indicado, assim utilizaremos a Integral Definida 

.

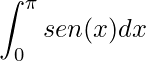O primeiro passo é encontrar a integral como vimos na Integral Indefinida e deixando indicado o intervalo de integração. Perceba que podemos integrar direto, sem uso de outro artificio, pois temos uma integral imediata

. 

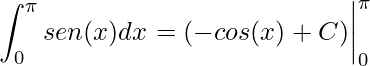O passo seguinte é aplicarmos o intervalo de integração, que consiste em aplicar o intervalo superior na função encontrada menos o intervalo inferior também aplicado na função encontrada

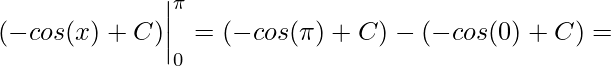
Logo,

.

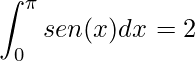Obs: perceba que a constante C que surge quando integramos sempre se cancelará nas integrais definidas, assim caso queira omitir não influenciará no resultado final.

Observe esta área no gráfico da função

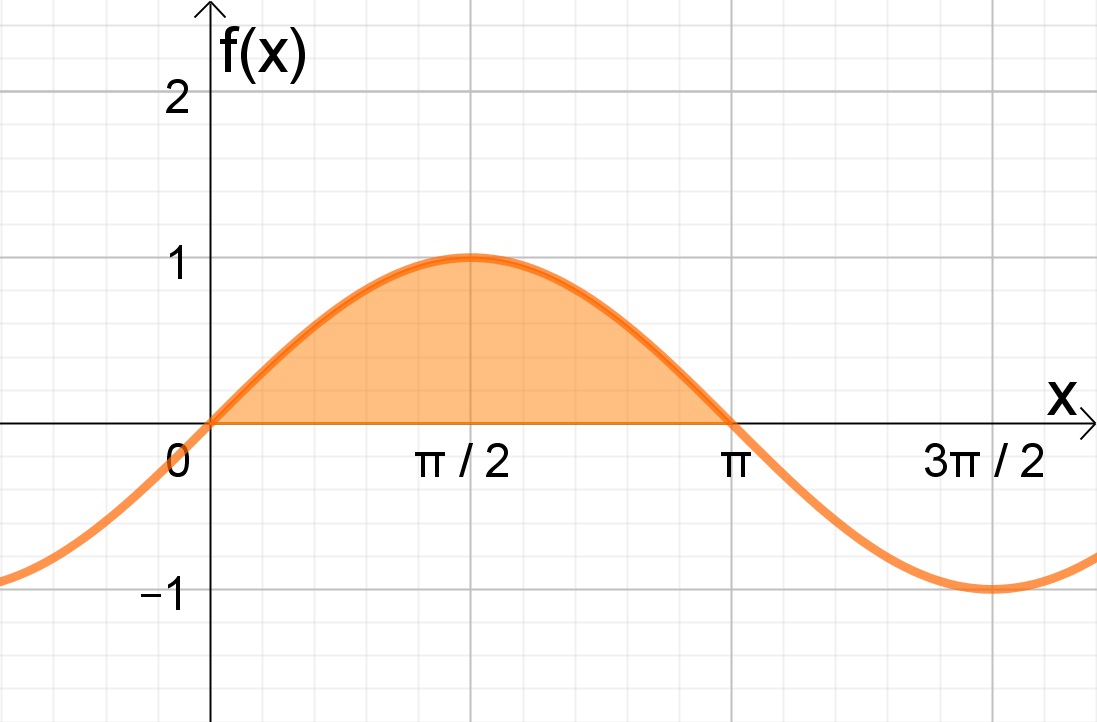
Atenção: No gráfico anterior, observe que o intervalo indicado fica todo sobre o eixo x. Assim aplicamos uma única integral para todo intervalo. Porém quando tivermos uma parte a cima o eixo x e outra a baixo, temos que separar os intervalos.

Para ficar mais claro a explicação utilizaremos outro exemplo.  

Exemplo 2: Encontre a área limitada pela função  e o eixo x no intervalo .

Observe que se aplicarmos a integral para todo o domínio teremos uma área nula

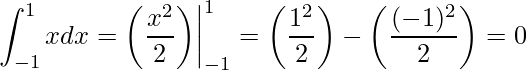
entretanto este resultado é falso. Isto ocorre pois a função ora é positiva e ora negativa. Para obtermos o verdadeiro resultado, devemos separa em duas integrais.

• Uma para o domínio onde a função é não positiva, .
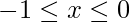• Uma para o domínio onde a função é não negativa, .

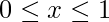Mas para onde a função é não positiva, a integral deve ser antecedida do sinal menos, pois se não a área será negativa neste intervalo devido a altura ser negativa. Assim temos que determinar

.

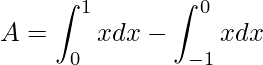Calculando separadamente

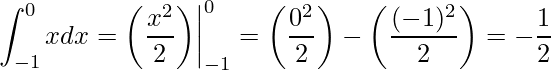
Substituindo obtemos o resultado esperado 

.

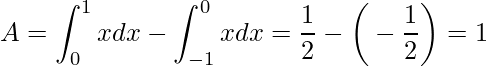No gráfico a seguir podemos perceber a veracidade do resultado, ao calcular, geometricamente, as áreas dos dois triângulos. 

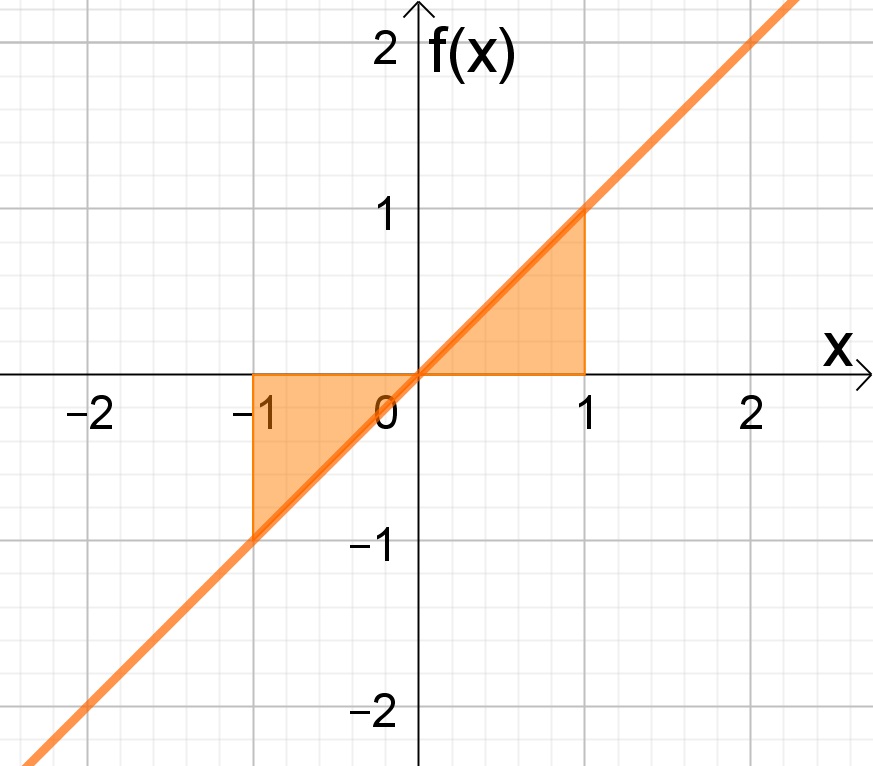
Acompanhe a resolução de outro exemplo clicando aqui.