Gráfico de Funções Polinomiais

O Gráfico de Funções Polinomiais é muito comum no estudo do cálculo, porque as funções polinomiais possuem poucas restrições na realização das operações matemáticas, o que torna seu estudo fundamental. 

Um caso particular das Funções Polinomias são as funções lineares (retas), funções quadráticas (parábolas), funções cúbicas e assim por diante.

Essas funções se caracterizam pela soma de potências da variável independente , da seguinte forma: 

,

onde  é a ordem ou o grau do polinômio e os  são constantes arbitrárias.  

A ordem do polinômio representa a quantidade de raízes que esta função possui. Lembrando que as raízes podem ser reais ou imaginárias. Então, quando forem reais, representam o ponto onde o gráfico corta o eixo .  

Veja o exemplo de um Gráfico de Funções Polinomiais de quinta ordem, na qual possui 3 raízes reais e duas imaginárias:

.

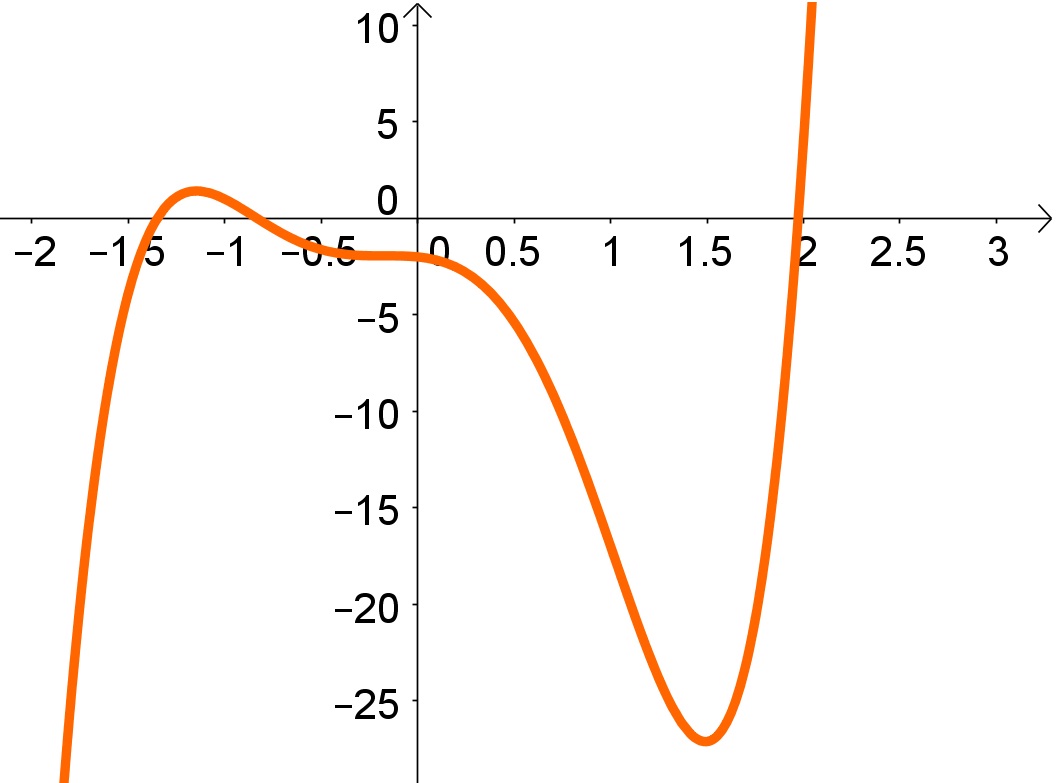
Obs: a quantidade de raízes imaginárias são sempre aos pares (2, 4, 6, …). 

Além disso, lembre que a ordem de um polinômio é determinada pelo termo que possuir a maior potência da variável independente  .

Gráfico de Funções Polinomiais de ordem par

O gráfico de funções de ordem par possui a característica que nas suas duas extremidades de , ou seja, ( e ). Logo, o gráfico da função tende para o mesmo valor.

Assim, caso a constante que acompanha o termo de maior ordem for positiva, as extremidades do gráfico vão para em  . Caso for negativa, o gráfico tende para . 

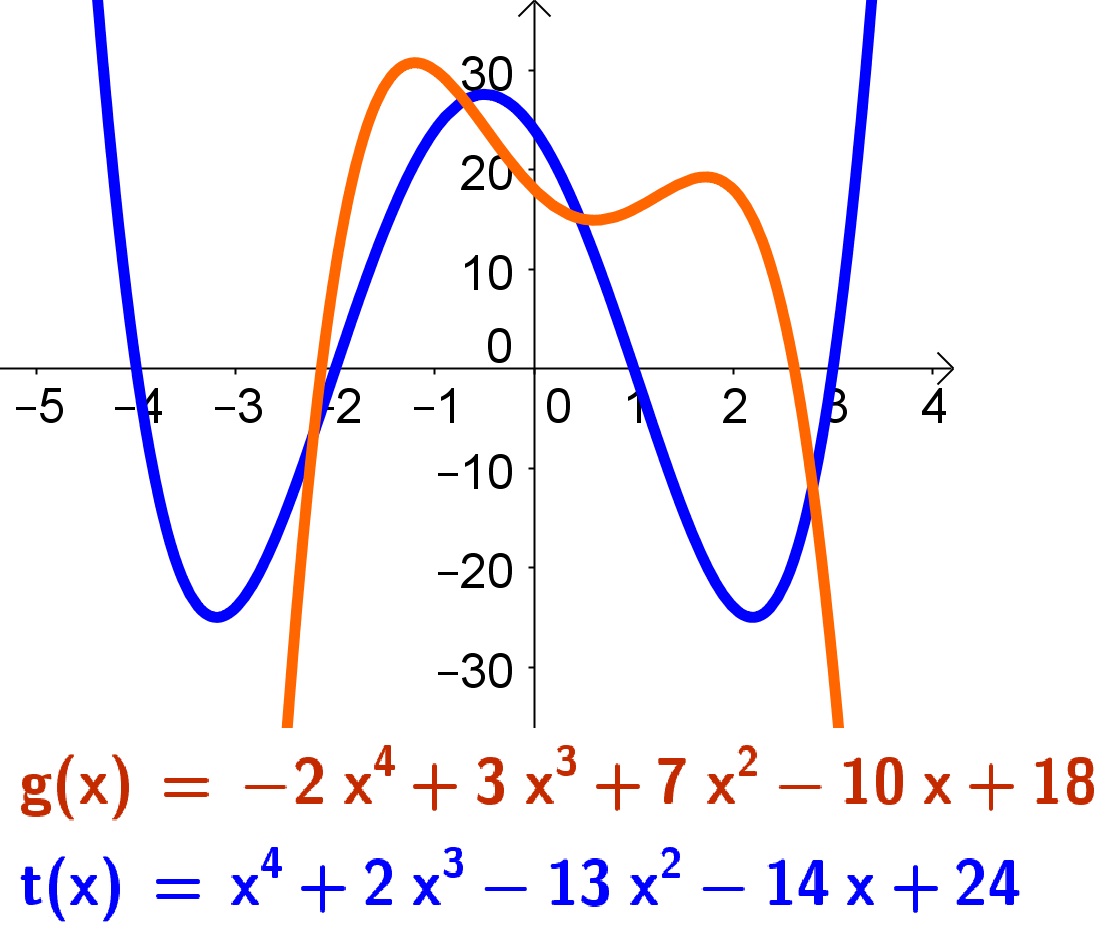
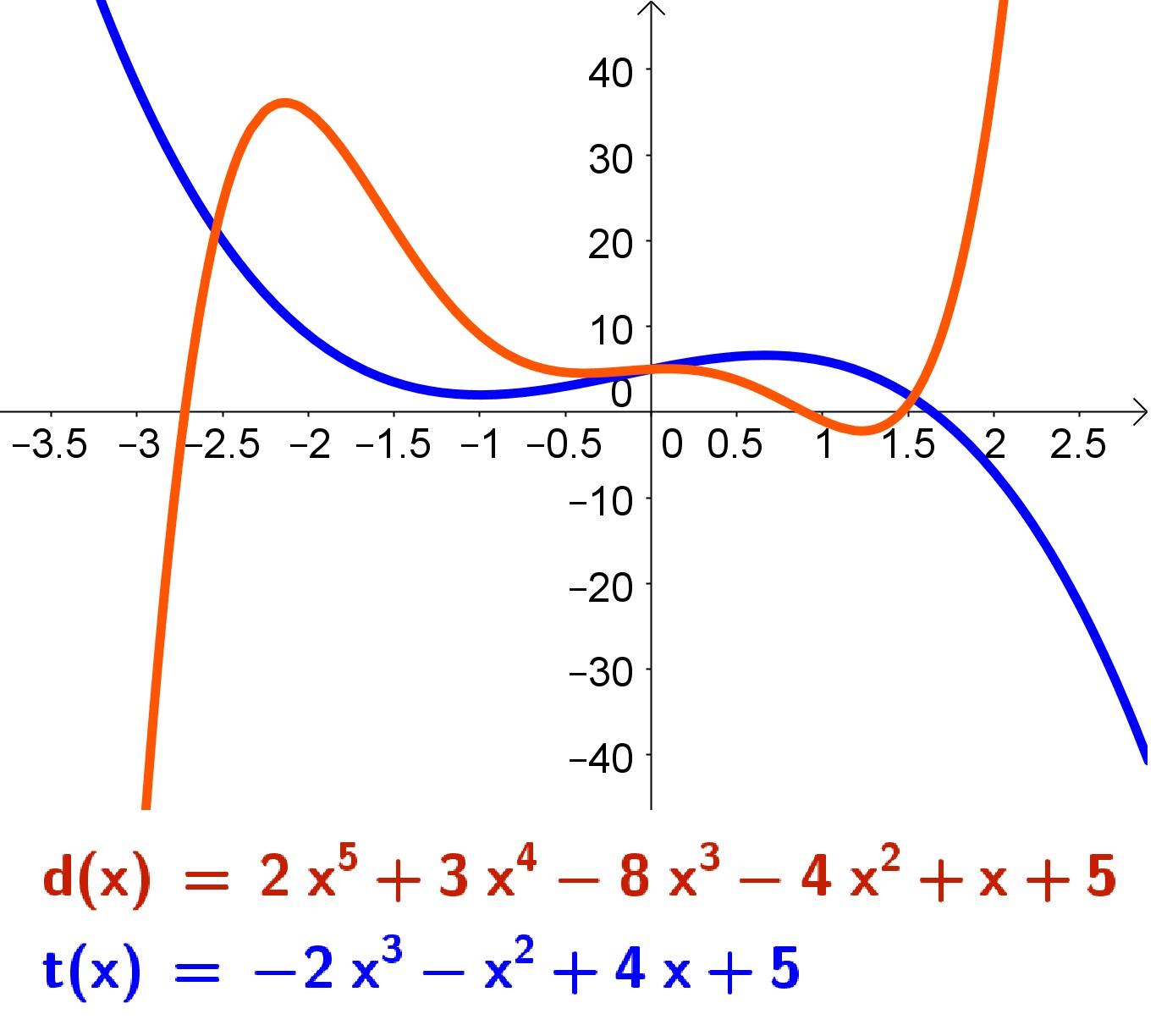
Gráfico de Funções Polinomiais de ordem Ímpar

O gráfico de funções de ordem ímpar possui a característica que cada uma das suas duas extremidades em , ou seja, ( e ). Logo o gráfico da função tende para extremos diferentes.

Assim, caso a constante que acompanha o termo de maior ordem for positiva, na extremidade de os valores de  tendem a . Na outra extremidade de , ou seja, os valores de tendem para .

Além do mais quando a constante que acompanha o termo de maior ordem for negativa o comportamento é inverso, conforme exemplo a seguir:

Observe que o termo independente de qualquer polinômio representa o ponto onde o gráfico corta o eixo .

Portanto, espero que tenha ficado claro esse post sobre o Gráfico de funções Polinomiais. Continuem nos acompanhando. Divulguem nosso site. Compartilhe esse post com os amigos ou com alguém que esse assunto possa ser relevante. Se ficou alguma dúvida, coloque nos comentários abaixo. Use seu login do Facebook.

Caso desejar, acompanhe também uma outra explicação sobre está temática em vídeo, clicando aqui.