aplicações >

Análise do crescimento e decrescimento de funções

Análise do crescimento e decrescimento de funções

Uma das aplicações das derivadas é a análise do crescimento e decrescimento de funções, ou seja, o sinal da derivada nos fornece onde a função é crescente (+) e decrescente (-). Este recuso é usado principalmente em funções em que temos dificuldade de construir o gráfico. Assim, a partir da derivada podemos construir o esboço das funções com mais detalhes. 

Definição de crescimento e decrescimento de funções 

Seja a função f(x) e dois pontos do domínio x_{1}<x_{2}, então dizemos que

  • A função f(x) é crescente nos intervalos onde f(x_{1})<f(x_{2});
  • A função f(x) é decrescente nos intervalos onde f(x_{1})>f(x_{2});
  • A função f(x) é constante nos intervalos onde f(x_{1})=f(x_{2}).

Agora relembre a definição de derivada para cada ponto c do domínio

{f}'(c)=\displaystyle\lim\limits_{x\rightarrow c}\frac{f(x)-f(c)}{x-c}.

Observe a relação que existe entre esta definição de derivada e a definição de crescimento/decrescimento de uma função. Assim podemos notar o porquê o sinal da deriva expressar o comportamento da função.

Teorema do comportamento das funções

Seja f(x) uma função continua no intervalo [a,b]  e derivável no intervalo (a,b) então

  • f(x) é crescente em todo x em que f'(x)>0;
  • f(x) é decrescente em todo x em que f'(x)<0;
  • f(x) é constante em todo x em que f'(x)=0.

Vejamos alguns exemplos para uma melhor compreensão.

1) f(x)=ax+b com a\neq 0: 

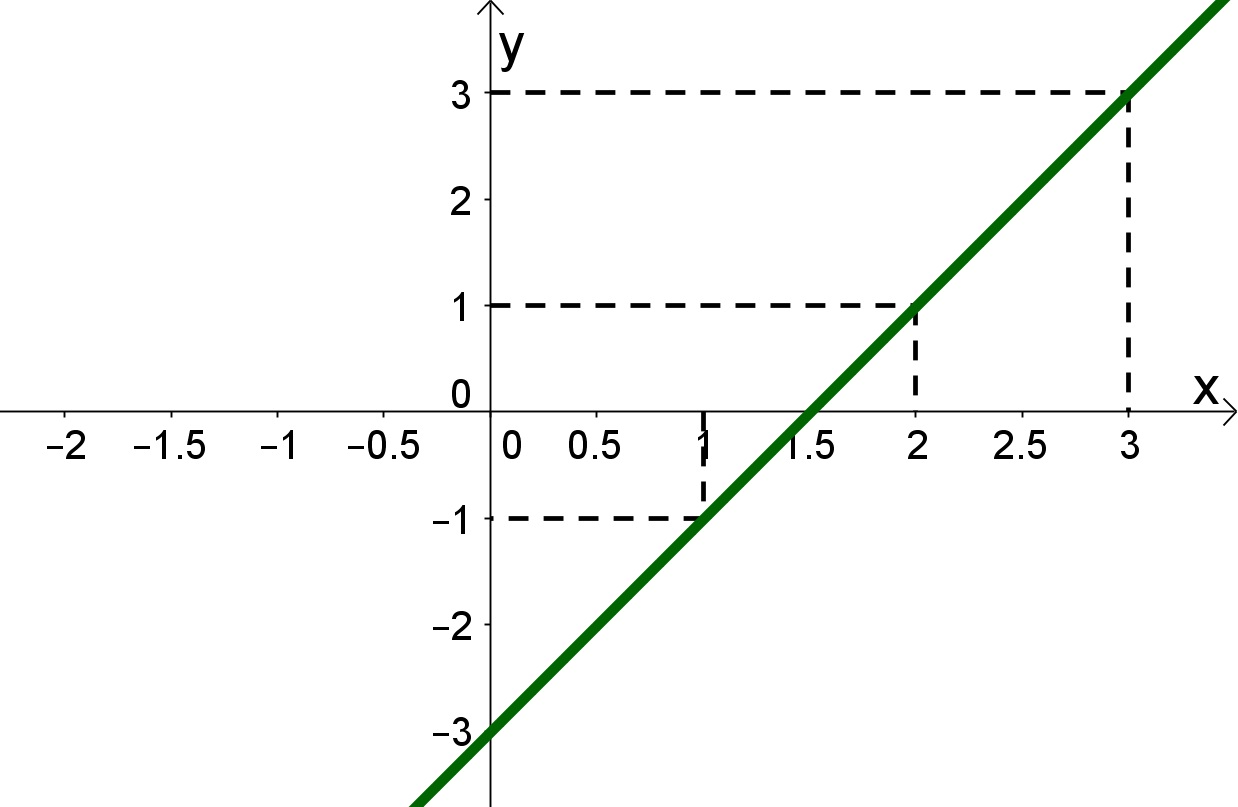
Neste exemplo temos a função básica da reta, que ao derivar temos 

f'(x)=a.

Como já esperávamos a função será crescente se a>0 e decrescente se a<0, pois a é o angular da reta. Veja o exemplo: f(x)=2x-3.

Análise do crescimento e decrescimento

2)  f(x)=e^{ax} com a\neq 0:

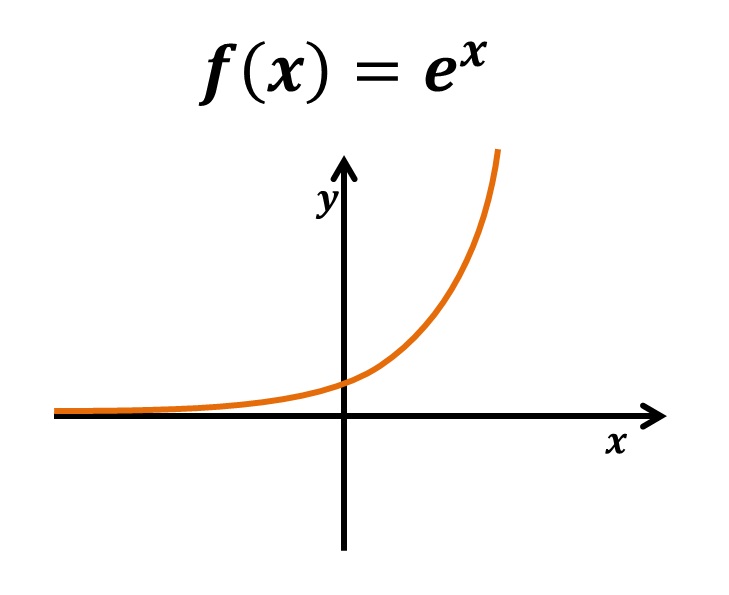
Outro exemplo clássico de funções que é funções exponenciais, que ao derivar temos 

f'(x)=ae^{ax}.

Como no exemplo anterior o valor de a é quem determina o comportamento: a função será crescente se a>0 e decrescente se a<0, pois e^{ax} será sempre positivo. Logo ao multiplicá-lo por a, este determinará o sinal.

Análise do crescimento e decrescimento

Acompanhe também explicações e resoluções de outros exemplos em vídeo, clicando aqui. 

Publicado em 04/12/2017, em aplicações, Derivadas.