Aproximação linear local – exemplos resolvidos
Aproximação linear local – exemplos resolvidos
Uma das aplicações de derivadas é a Aproximação linear local, que consiste em aproximar uma função qualquer por uma função linear. Entretanto, haverá apenas uma boa aproximação local, ou seja, apenas na vizinhança de onde está sendo feita a aproximação.
Exemplos resolvidos de Aproximação linear local
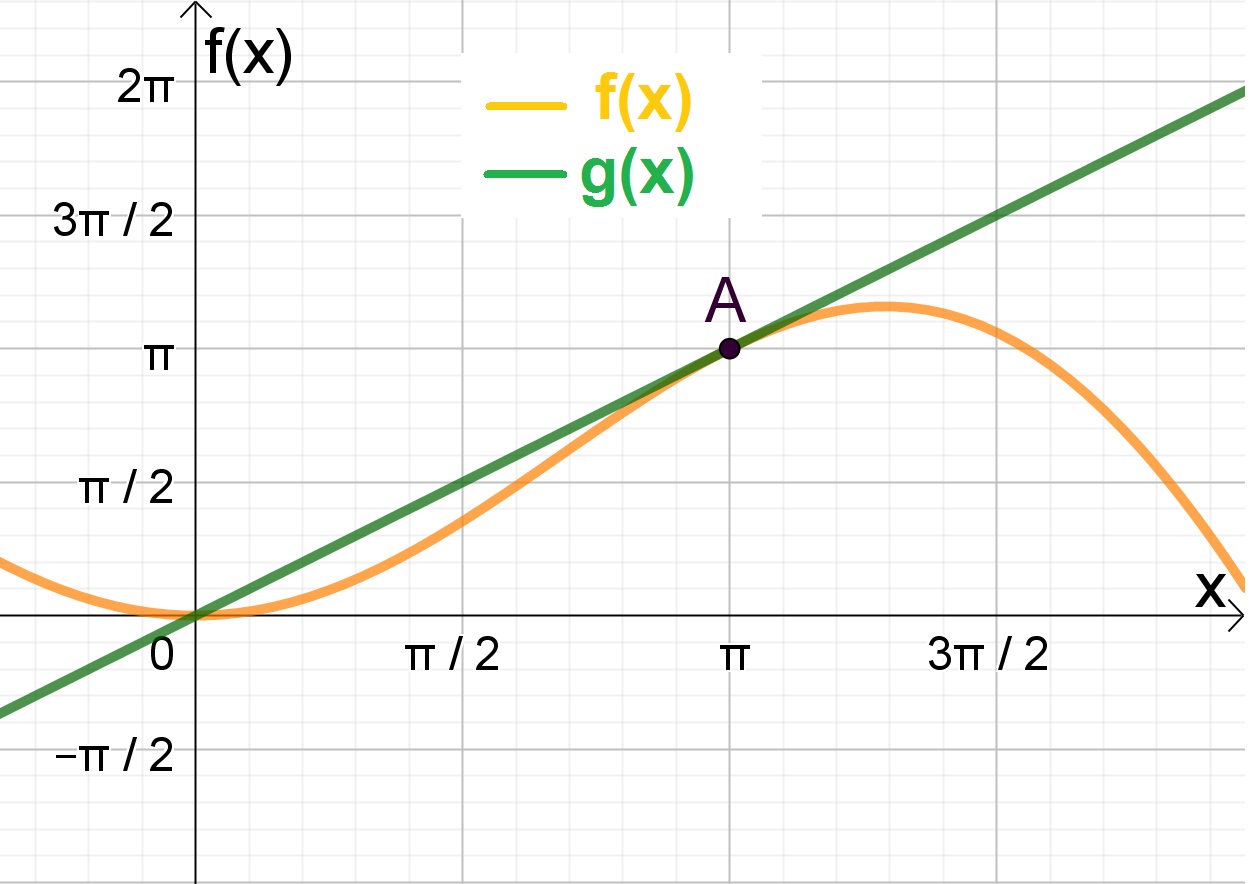
1) Obtenha uma aproximação linear da função 
O primeiro passo é derivar a função dada, na qual devemos aplicar a regra do produto
![\displaystyle f'(x)=\frac{d}{dx}\left [x \right ]sen\left (\frac{x}{2} \right )+x\ \frac{d}{dx}\left [sen\left (\frac{x}{2} \right ) \right ]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+f%27%28x%29%3D%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft+%5Bx+%5Cright+%5Dsen%5Cleft+%28%5Cfrac%7Bx%7D%7B2%7D+%5Cright+%29%2Bx%5C+%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft+%5Bsen%5Cleft+%28%5Cfrac%7Bx%7D%7B2%7D+%5Cright+%29+%5Cright+%5D&bg=ffffff&fg=000000&s=1 "\displaystyle f'(x)=\frac{d}{dx}\left [x \right ]sen\left (\frac{x}{2} \right )+x\ \frac{d}{dx}\left [sen\left (\frac{x}{2} \right ) \right ]")
![\displaystyle =sen\left (\frac{x}{2} \right )+x\ \frac{d}{dx}\left [sen\left (\frac{x}{2} \right ) \right ]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%3Dsen%5Cleft+%28%5Cfrac%7Bx%7D%7B2%7D+%5Cright+%29%2Bx%5C+%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft+%5Bsen%5Cleft+%28%5Cfrac%7Bx%7D%7B2%7D+%5Cright+%29+%5Cright+%5D&bg=ffffff&fg=000000&s=1 "\displaystyle =sen\left (\frac{x}{2} \right )+x\ \frac{d}{dx}\left [sen\left (\frac{x}{2} \right ) \right ]")
Observe que no segundo termo devemos aplicar a regra da cadeia, onde usamos
![\displaystyle f'(x)=sen\left (\frac{x}{2} \right )+x\ \frac{d}{du}\left [sen(u) \right ]\cdot \frac{d}{dx}\left [\frac{x}{2} \right ]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+f%27%28x%29%3Dsen%5Cleft+%28%5Cfrac%7Bx%7D%7B2%7D+%5Cright+%29%2Bx%5C+%5Cfrac%7Bd%7D%7Bdu%7D%5Cleft+%5Bsen%28u%29+%5Cright+%5D%5Ccdot+%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft+%5B%5Cfrac%7Bx%7D%7B2%7D+%5Cright+%5D&bg=ffffff&fg=000000&s=1 "\displaystyle f'(x)=sen\left (\frac{x}{2} \right )+x\ \frac{d}{du}\left [sen(u) \right ]\cdot \frac{d}{dx}\left [\frac{x}{2} \right ]")
e substituindo teremos
O segundo passo é encontrar o coeficiente angular da reta tangente através da aplicação do ponto
O terceiro passo e último é encontrar o coeficiente linear, onde temos o ponto
assim substituindo na formula geral da equação linear
Portanto, Aproximação linear local da função dada no ponto
Observe no gráfico a seguir as duas funções e como esta aproximação é boa para uma certa vizinhança do ponto desejado.
2) Obtenha uma aproximação linear da função ![\displaystyle f(x)=\sqrt[3]{x^{2}-1}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+f%28x%29%3D%5Csqrt%5B3%5D%7Bx%5E%7B2%7D-1%7D&bg=ffffff&fg=000000&s=1 "\displaystyle f(x)=\sqrt[3]{x^{2}-1}")
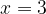Este exercício resolveremos utilizando a mesma sequência de passos do exercício anterior. Assim iniciamos derivando a função dada, onde devemos aplicar a regra da cadeia e usando
![\displaystyle f'(x)= \frac{d}{du}\left [\sqrt[3]{u} \right ]\cdot \frac{d}{dx}\left [x^{2}-1 \right ]=\frac{u^{-\frac{2}{3}}}{3}\cdot 2x](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+f%27%28x%29%3D+%5Cfrac%7Bd%7D%7Bdu%7D%5Cleft+%5B%5Csqrt%5B3%5D%7Bu%7D+%5Cright+%5D%5Ccdot+%5Cfrac%7Bd%7D%7Bdx%7D%5Cleft+%5Bx%5E%7B2%7D-1+%5Cright+%5D%3D%5Cfrac%7Bu%5E%7B-%5Cfrac%7B2%7D%7B3%7D%7D%7D%7B3%7D%5Ccdot+2x&bg=ffffff&fg=000000&s=1 "\displaystyle f'(x)= \frac{d}{du}\left [\sqrt[3]{u} \right ]\cdot \frac{d}{dx}\left [x^{2}-1 \right ]=\frac{u^{-\frac{2}{3}}}{3}\cdot 2x")
Substituindo e manipulando a equação obteremos
![\displaystyle f'(x)=\frac{2x}{3\sqrt[3]{(x^{2}-1)^{2}}}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+f%27%28x%29%3D%5Cfrac%7B2x%7D%7B3%5Csqrt%5B3%5D%7B%28x%5E%7B2%7D-1%29%5E%7B2%7D%7D%7D&bg=ffffff&fg=000000&s=1 "\displaystyle f'(x)=\frac{2x}{3\sqrt[3]{(x^{2}-1)^{2}}}")
Assim para encontrar a coeficiente angular da reta devemos aplicar o ponto
![\displaystyle f'(3)=\frac{2\cdot 3}{3\sqrt[3]{(3^{2}-1)^{2}}}=\frac{1}{2}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+f%27%283%29%3D%5Cfrac%7B2%5Ccdot+3%7D%7B3%5Csqrt%5B3%5D%7B%283%5E%7B2%7D-1%29%5E%7B2%7D%7D%7D%3D%5Cfrac%7B1%7D%7B2%7D&bg=ffffff&fg=000000&s=1 "\displaystyle f'(3)=\frac{2\cdot 3}{3\sqrt[3]{(3^{2}-1)^{2}}}=\frac{1}{2}")
E para encontrar o coeficiente linear devemos ter o valor de y no ponto desejado
![\displaystyle f(3)=\sqrt[3]{3^{2}-1}=2](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+f%283%29%3D%5Csqrt%5B3%5D%7B3%5E%7B2%7D-1%7D%3D2&bg=ffffff&fg=000000&s=1 "\displaystyle f(3)=\sqrt[3]{3^{2}-1}=2")
assim substituindo da formula geral da equação linear
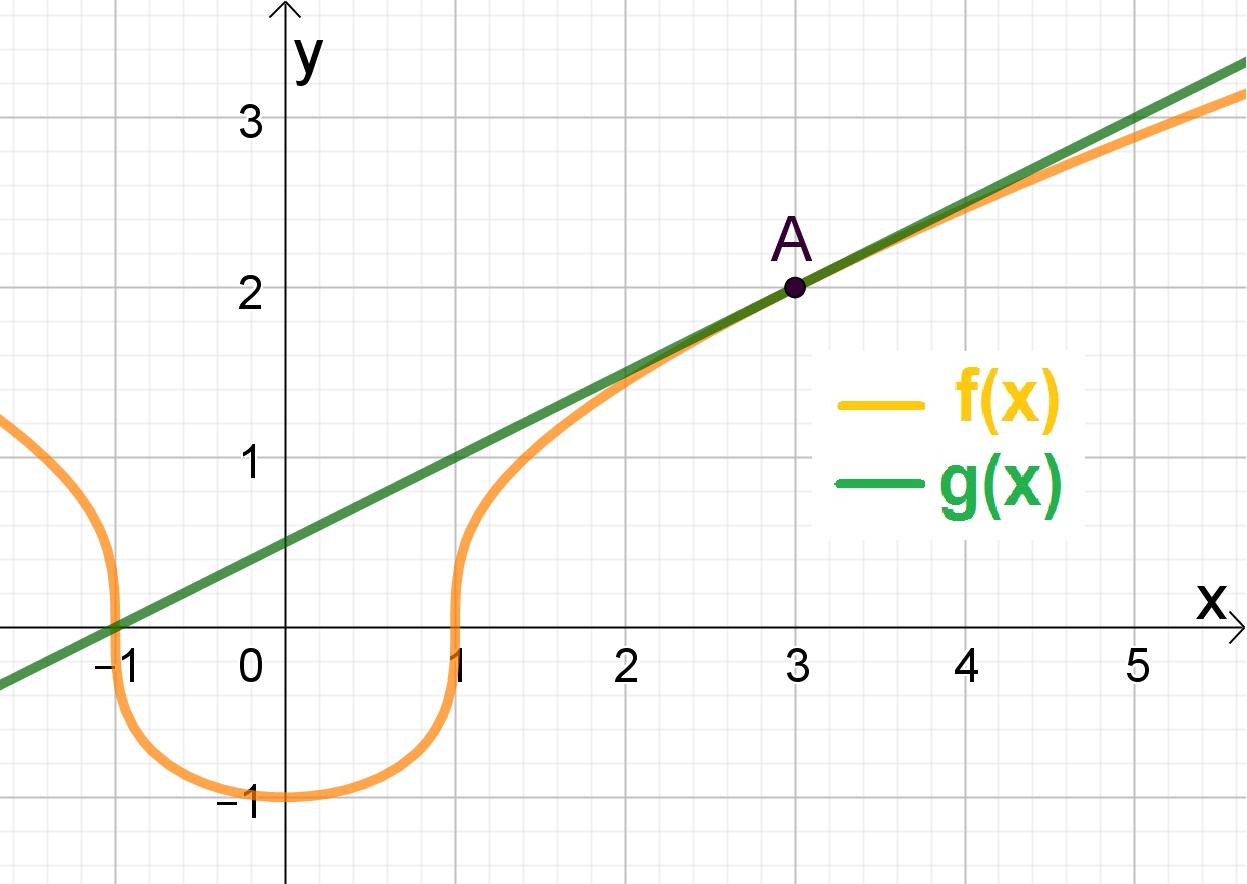
Portanto, Aproximação linear local da função dada no ponto
Observe no gráfico a seguir as duas funções e como esta aproximação é boa para uma certa vizinhança do ponto desejado. Entretanto, esta vizinhança é maior daquela do exercício anterior, visto o comportamento mais suave da função no ponto desejado.
Acompanhe a resolução de outros exercícios em vídeo clicando aqui.
