Comprimento de uma função no plano –
comprimento de arco
O cálculo do Comprimento de uma função no plano é como medirmos um barbante que não está esticado, mas todo ondulado. Assim, conforme a complexidade da curva, mais difícil pode se tornar o cálculo. A fim de resolver este problema de forma geral utiliza-se as integrais. A ideia é a mesma das outras aplicações das integrais, que é o fatiamento em pequenos intervalos.
Definindo o Problema
Seja uma função f(x) definida entre [a,b] e queremos calcular seu comprimento. Determine uma fórmula geral para qualquer função arbitrária que seja continua no intervalo indicado.
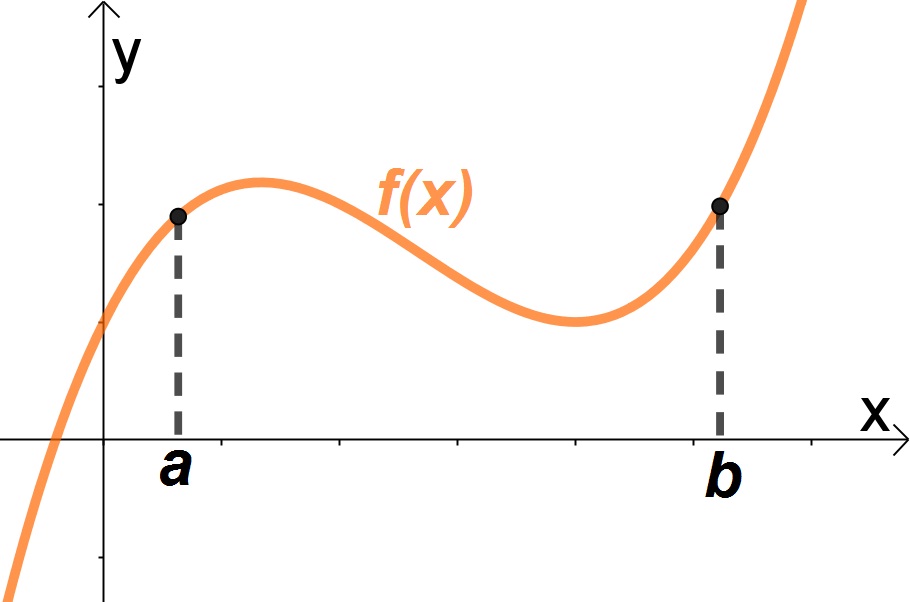
Deduzindo a fórmula Comprimento de uma função no plano
Seja f(x) uma função contínua em [a,b] e com sua derivada contínua em ]a,b[. Devemos dividir o domínio em n intervalos: . Em seguida, traçar uma reta entre os pontos de cada intervalo, ou seja,
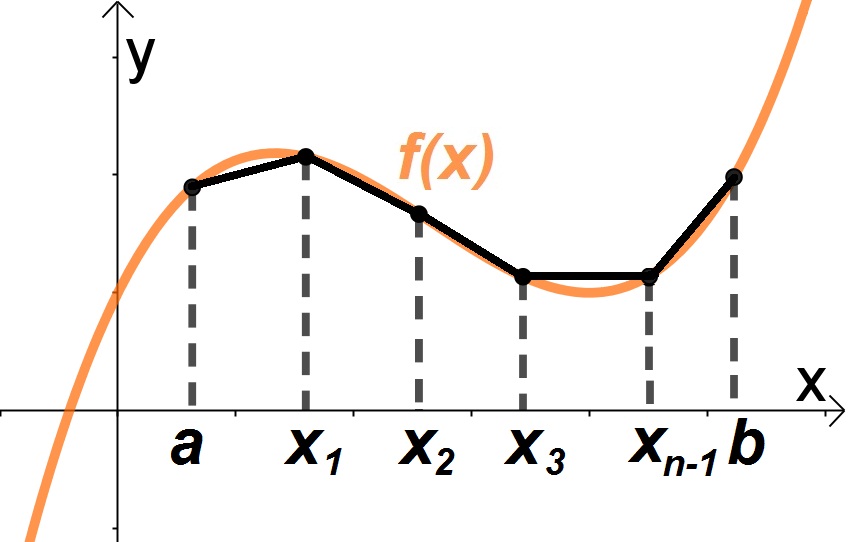
Obtendo assim os pontos , onde
. Observe que o comprimento de cada seguimento é dado pelo Teorema de Pitágoras
onde .
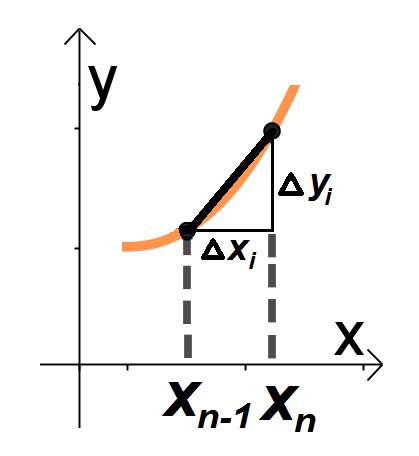
Em seguida, somamos todos os intervalos
.
Pelo Teorema do Valor Médio sabemos que existe um tal que
.
Substituindo teremos
.
Tomando o limite de temos o comprimento da função
.
De forma análoga podemos construir a dedução para funções f(y).


