Volumes e sólidos de revolução – volume por fatiamento

A base do cálculo dos Volumes e sólidos de revolução está em fatiar o domínio em fatias finas. Entretanto, devemos saber calcular a área de cada secção transversal (fatia), para multiplicar cada uma pela sua espessura. Em seguida, formar uma soma de Riemann e fazer a espessura tender a zero (limite).  Na linguagem matemática é expressa da seguinte forma

.

Onde  é a função que descreve a área da fatia no ponto  que pertence ao intervalo i. Observe que estamos tratando do caso da revolução entorno do eixo x, para o caso no eixo y será tratado em outra postagem. 

Definição de sólidos de revolução

Os sólidos de revolução são aqueles gerados ao rotacionar uma área em torno de um eixo, que está no mesmo plano da área. Veja figura a seguir:

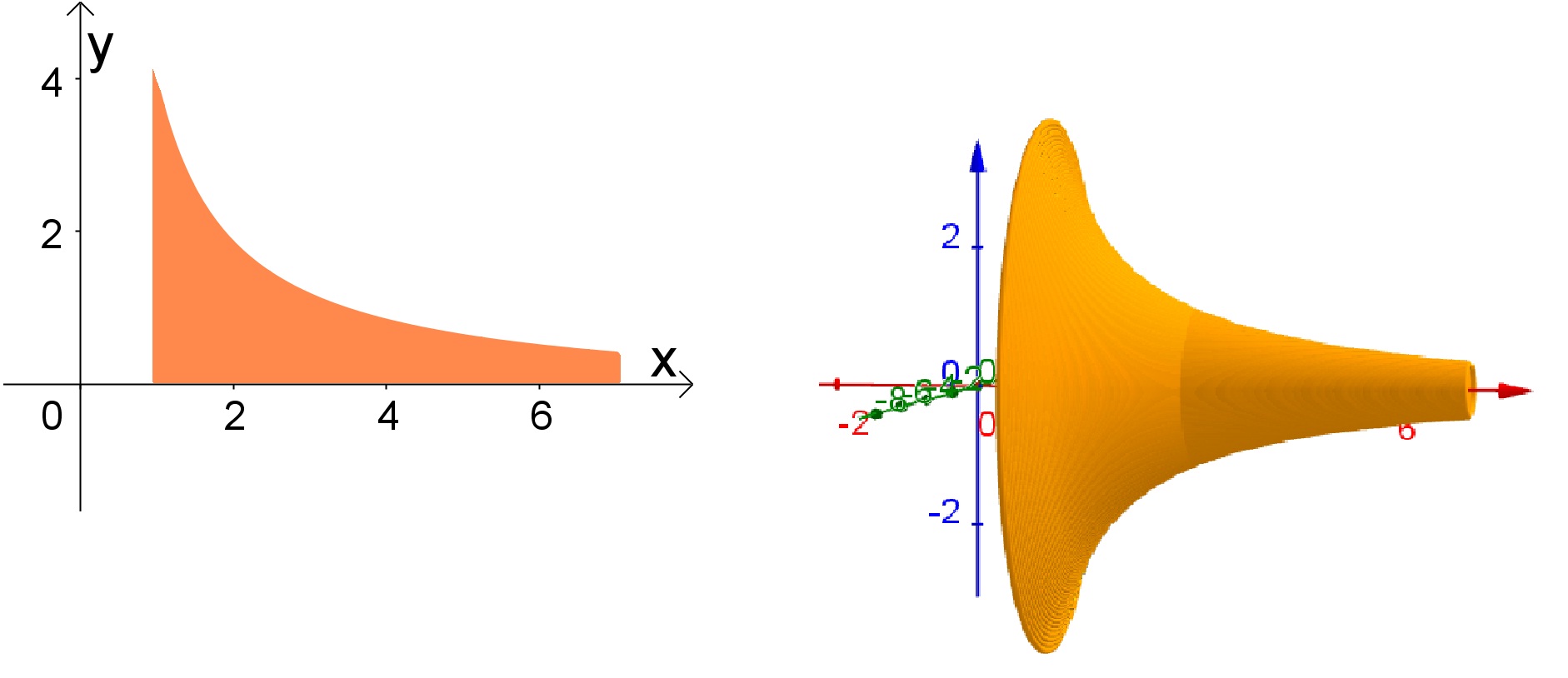
Definição da fórmula do Volumes

Seja um volume delimitado por dois planos perpendiculares ao eixo x entre x=a e x=b.  E seja A(x) a área de cada secção transversal do volume o perpendiculares ao eixo x, então o volume deles é dado

.

Desde que, A(x) seja integrável no domínio.

Definição da fórmula do Volumes dos sólidos de revolução

Seja S a área limitada pela função f(x) continua não negativa, o eixo x e as retas x=a e x=b.  Assim, o sólido de revolução gerado pela rotação da área S entorno do eixo x é dado

.

Obs: Esta segunda fórmula tem por base a primeira, pois a área A(x) são círculos de raio f(x). Lembre que a fórmula da área dos círculos é dada por 

.

Exemplo: a fórmula do volume de uma esfera que aprendemos no ensino médio é uma aplicação destas integrais.  Tomando a equação do circulo centrada na origem 

onde r é o raio. Isolando a variável y e tomando apenas a parte positiva temos 

.

Dessa forma, o sólido formado ao rotacionar y=f(x) em torno do eixo x é uma esfera de raio r. Aplicando na fórmula do Volumes dos sólidos de revolução temos 

.

Integrando temos o resultado

.

Acompanhe a resolução de outros exercícios clicando aqui.