Logaritmos: contexto histórico e aplicações do cotidiano

Conforme o ilustríssimo Elon Lages Lima, os logaritmos – que durante três séculos e meio tão bem desempenharam o papel de maravilhoso instrumento para simplificar o cálculo aritmético, permitindo que se efetuassem, com rapidez e precisão, operações complicadas como a multiplicação de dois números com muitos algarismos, ou uma potenciação com expoente fracionário perderam, há algum tempo, esse lugar de eficiente calculador.

Isso aconteceu pois seu lugar foi ocupado com grande êxito pelas computadores e calculadoras científicas.

Apesar disso, os logaritmos continuam, por motivos bem diversos, a merecer uma posição de destaque no ensino da Matemática, devido à posição central que ocupam nesta ciência e em suas aplicações.

Essa posição é permanente, porque a função logarítmica e a sua inversa, a função exponencial, constituem a única maneira de se escrever matematicamente a evolução de uma grandeza cuja taxa de crescimento ou decrescimento é proporcional à quantidade daquela grandeza existente num dado momento.

Além disso, para transformar a multiplicação em adição, para saber em quanto tempo você vai acumular uma certa quantia de dinheiro, para detectar fraudes, medir a intensidade de terremotos e entender os nossos sentidos, essas são só algumas aplicações dos logaritmos.

Ah então você gosta de matemática?

Pois é, tem louco para tudo nessa vida.

Faz uma conta aí para mim então: quanto que é 1548 x 982. Se tem uma coisa que as pessoas odeiam é fazer conta. É chato, dá trabalho e ainda tem o risco de você errar.

Agora imagine você vivendo lá no século 16 quando não tinha calculadora.

grandes descobertas

Existia uma necessidade muito grande de se desenvolver novas tecnologias, principalmente por causa das grandes navegações. Era uma coisa terrível. Por isso, perdia-se, em média, 15 meses fazendo os cálculos.

Naquela época o máximo que você tinha era um ábaco ou então algumas identidades trigonométricas. Então, foi nesse contexto que surgiu o grande Jonh Napier, considerado o inventor dos logaritmos.

John Napier

Ele foi um matemático – astrônomo escocês que tinha fortes interesses teológicos e um lado um pouco místico. Reza a lenda que andava com uma aranha preta dentro de uma caixinha no bolso e que ele tinha um companheiro mágico que era um galo.

Os boatos dizem que ele usava esse galo para descobrir quais eram os empregados que estavam roubando ele.

Os empregados suspeitos eram trancados dentro de um quarto junto com o galo e ele dizia: eu quero que cada um de vocês pegue o galo nas mãos, pois no final com toda certeza descobrirei quem é o culpado.

Jonh Napier o pai dos logaritmos — Jonh Napier

O engraçado é que o galo descobria mesmo, mas ele tinha um truque claro.

Ele sabia que o culpado iria ficar com medo de pegar o galo nas mãos, assim ele colocava uma fina camada de fuligem em cima do galo e depois ele olhava quem estava com as mãos limpas. Essa pessoa com certeza era o culpado.

Deixando de lado essas bizarrices, Napier descobriu que poderia simplificar os cálculos transformando as multiplicações em somas. E para isso ele usava as propriedades da potenciação. Vamos mostrar isso utilizando as potências de 2.

Por exemplo, sabemos que

$\displaystyle 2\times 4=8$ .

Perceba que $\displaystyle 2=2^1$ e $\displaystyle 4=2^2$ , ou seja:

$\displaystyle 2^1 \times 2^2 = 2^3 = 8$ .

Olhando os expoentes das potencias percebemos que é como se estivéssemos somando $\displaystyle 1+2=3$ .

Isso acontece com os outros expoentes também. Então, se quisermos saber quanto que é $\displaystyle 32 \times 64$ podemos transformar os números em potências de 2 e somar os expoentes para descobrir o resultado.

Em outras palavras, $\displaystyle 32=2^5$ e $\displaystyle 64=2^6$ . O resultado vai ser

$\displaystyle 2^5 \times 2^6=2^{11}$ .

No entanto, isso não ajuda muito se não soubermos quanto que é $\displaystyle 2^{11}$ , concorda?

A grande ideia

E aí que vem a grande sacada. É só construir uma tabela com o valor das potências de 2. Se quisermos saber agora quanto é $\displaystyle 128 \times 32$ basta procurar na tabela quais são as potências correspondentes.

$\displaystyle 2^1=2 \\ 2^2=4 \\2^3=8 \\ 2^4=16\\ 2^5=32\\ 2^6=64 \\ 2^7=128\\ 2^8=256 \\ 2^9=512 \\ 2^{10}=1024 \\ 2^{11}=2048 \\ 2^{12}=4096 \\ \vdots$ .

Nesse caso, $\displaystyle 128= 2^7$ e $\displaystyle 32=2^5$ . Basta somar $\displaystyle 7+5=12$ . Logo, o resultado vai ser

$\displaystyle 128 \times 32 = 2^7 \times 2^5 = 2^{12}$ .

Se voltarmos na tabela para descobrir qual é o valor de $\displaystyle 2^{12}$ vemos que é 4096, muito mais rápido do que calcular na mão, concorda?

Deu-se o nome a esses expoentes de logaritmos. Por isso, nós dizemos que o logaritmo de 32 na base 2 = 5.

Em outras palavras, qual o expoente que eu preciso elevar a dois para que dê 32? Matematicamente isso quer dizer:

$\displaystyle \log_{2} 32 \Leftrightarrow 2^x=32$ .

Sabemos que a resposta é 5, pois $\displaystyle 2^5=32$ , logo:

$\displaystyle \log_{2} 32=5$ .

Da mesma forma,

$\displaystyle \log_{2} 128 \Leftrightarrow 2^x=128$ .

Como $\displaystyle 2^x=128 \Leftrightarrow 2^x=2^7$ , temos que $\displaystyle x=7$ . Portanto,

$\displaystyle \log_{2} 128 =7$ .

Usando essa mesma ideia, podemos observar também que

$\displaystyle \log_{2} 4096 =12$ .

Com isso podemos escrever que

$\displaystyle \log_{2} (32\times 128) = \log_{2} 32+ \log_{2} 128$ ,

que é uma propriedade bem importante dos logaritmos. Fizemos um exemplo com base 2 mas poderia ser qualquer outro número maior do que 1. Então, de uma forma geral temos que

$\displaystyle \log_{b} (X\times Y) = \log_{b} X+ \log_{b} Y$ .

Note que estamos transformando uma multiplicação em uma soma. Além de Napier outros matemáticos também dedicaram seu tempo para construir tabela de logaritmos.

Existem diversos livros que são conjuntos de tabelas de logaritmos em diversas bases. Até pouco tempo atrás, na década de 70, ainda se usava bastante essas tabelas de logaritmos.

Hoje, graças a Deus, temos as calculadoras e os computadores que vieram para facilitar nossas vidas.

No entanto, logaritmos são muito mais que só simplificar contas.

Existem diversas aplicações, sendo uma delas ligadas as aplicações financeiras.

Logaritmos na Matemática Financeira

Como você é uma pessoa que pensa no futuro, você quer saber quanto tempo você tem que deixar o seu dinheiro em algum investimento para que você consiga juntar, por exemplo, R$ 1.000.000,00.

Admitamos que com muito custo e suor você conseguiu juntar R$ 10.000,00 e supondo que a taxa de juros ao ano de um investimento seja de 7% ao ano.

Como calcular o tempo necessário para esses 10 mil se tornarem 1 milhão? .

Admitindo que o capital seja aplicado a juros compostos temos que usar a fórmula do Valor Futuro (montante), ou seja:

$\displaystyle FV=PV(1+i)^n$ ,

onde $FV$ é o valor futuro (montante), $PV$ é o Valor Presente (capital inicial), $i$ é a taxa de juros unitária e $n$ é o prazo (tempo).

Logo, $\displaystyle FV=1.000.000,00$ , $\displaystyle PV=10.000,00$ , $i=7 \%=0,07$ e $n$ é o que queremos saber.

Assim, substituindo os valores temos:

$\displaystyle 1.000.000,00=10.000,00(1+0,07)^n$ ,

que pode ser reescrita como

$\displaystyle 100=(1,07)^n$ .

Queremos encontrar o $n$ , então aplicando o logaritmo na base 10 (por conveniência) dos dois lados temos

$\displaystyle log(100)=log[(1,07)^n]$ .

Aqui cabe ressaltar que, uma vez que a base 10 é uma das mais comuns, convencionou-se

$\displaystyle log_{10} (x) = log (x)$ .

Em outras palavras, quando a base for 10 não precisa-se escrever, porque está subentendido.

Utilizando a Propriedade 2 dos Logaritmos , nós conseguimos isolar o $\displaystyle n$ que queremos calcular como:

$\displaystyle log(100)=n\times log(1,07)$ ,

ou seja,

$\displaystyle n=\frac{log(100)}{log(1,07)}$ .

Bem, temos

$\displaystyle log(100)=log_{10} (100) = 2$ ,

pois,

$\displaystyle 10^2=100$ .

Já para $\displaystyle log(1,07)$ , preciamos saber qual $\displaystyle x$ satisfaz

$\displaystyle 10^x=1,07$ .

Para isso, usa-se uma calculadora científica, na qual obtemos

$\displaystyle log(1,07)= 0,02938377768520964083454123946144$ ,

usando todos os dígitos da calculadora do computador.

Logo,

$\displaystyle n= \frac{log(100)}{log(1,07)}=\frac{2}{0,02938377768520964083454123946144} \cong 68,08$ ,

arredondando na segunda casa. Ou seja, levaria 68 anos para acumular 1 milhão com um investimento de 10 mil a uma taxa de 7% ao ano.

Logartimos na Lei de Benford

Suponha que você pegue uma lista com a população de todos os municípios do Estado de São Paulo. Existe um fato muito curioso relacionado aos logaritmos.

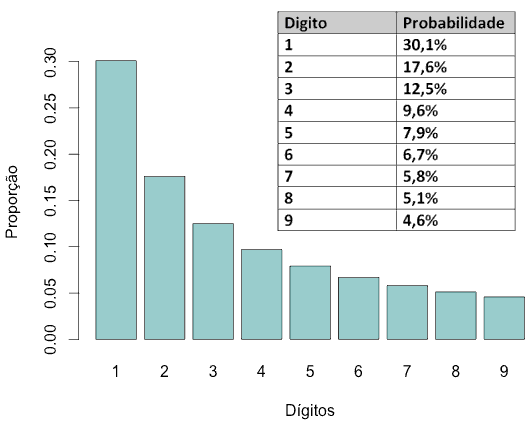
Se você contar quantas vezes aparece o algarismo 1 como o primeiro dígito, quantas vezes aparece o algarismo 2 com primeiro dígito, quantas vezes aparece o algarismo 3 como terceiro dígito das populações das cidades você vai perceber que:

1 aparece muito mais vezes que o 2; 2 aparece muito mais vezes que o 3; 3 aparece muito mais vezes que o 4 e assim por diante, até chegar no 9.

Isso é muito bizarro, porque o que espera-se é que a distribuição seja igual entre os algarismos, uma vez que estamos pegando o primeiro algarismo das cidades e esses números, a priori, são aleatórios.

Isso acontece com várias outras listas de números aleatórios da vida real. Se você quiser você mesmo pode conferir isso.

Entra lá no site do IBGE e baixa a lista da população por estado. E conta o número de algarismos 1 nessa lista. Dá para usar o Excel fazendo umas fórmula e você descobre esse fenômeno.

Isso se chama Lei de Benford.

Frank Benford demonstrou que esse resultado se aplica a uma ampla variedade de conjuntos de dados, incluindo contas de eletricidade, endereços, preços de ações, preços de casas, números de população, taxas de mortalidade, comprimentos de rios, constantes físicas e matemáticas. pelas leis de potência (que são muito comuns na natureza).

Todas essas afirmações são calculadas ou definidas junto a uma escala logarítmica.

A probabilidade se sair cada um dos dígitos é dado por:

$\displaystyle P(d) = log \left (1+\frac{1}{d}\right)$ ,

onde d é a probabilidade de sair cada um dos nove dígitos. O resultado vai ter uma distribuição semelhante a esta

Tudo bem, mas para que que serve isso?

Pode servir para detectar fraudes, por exemplo. Se você utilizar o mesmo raciocínio de cidades e verificar a votação das eleições para presidente de um país.

Os votos de cada urna devem seguir a Lei de Benford, ou seja, se não tiver essa distribuição, existe um risco da eleição ter sido fraudada.

O mesmo vale para as declarações de imposto de renda e para contabilidade de um modo geral.

Se você calcular o primeiro dígito nas potências de 2 ou na sequência de Fibonacci, você vai ver que também aparece essa mesma distribuição, o que é realmente muito interessante.

Logaritmos na escala Richter

Escala Richter - aplicações logaritmos

Para construir a escala Richter que mede a intensidade dos terremotos, foi construída uma escala logarítmica que mede o nível da intensidade sonora que ouvimos.

Aliás, os nossos sentidos humanos de uma forma geral segue uma escala logarítmica que é descrita pela lei de Weber-Fechner .

A lei de Weber-Fechner pode ser enunciada como: “a resposta a qualquer estímulo é proporcional ao logaritmo da intensidade do estímulo”.

Esta lei aplica-se aos 5 sentidos, mas as suas implicações são mais bem entendidas quando se refere aos estímulos provocados pela luz e pelo som.

É decorrente do fenômeno assim descrito, que são medidas de percepção da intensidade sonora pelo ouvido humano, e luminosa pelos órgãos de visão, são feitas por grandezas logarítmicas.

É o caso do Decibel (dB) definido como 10 vezes o logaritmo decimal da intensidade sonora.

A mesma grandeza logarítmica descreve também a intensidade luminosa percepcionada, sendo genericamente usada em óptica e engenharia.

Logaritmos e o Decaimento Radioativo

A meia vida de um material radioativo é o tempo necessário para que uma quantidade desse material decaia à metade de sua quantidade original.

Além do mais, qualquer material radioativo que se desintegre segue a seguinte lei de acordo com a equação abaixo:

$\displaystyle \frac{d Q(t)}{dt}=-r \times Q(t)$ ,

onde $\displaystyle Q(t)$ é a quantidade de material radioativo e $\displaystyle r$ é a constante de decaimento.

Admitindo que a quantidade inicial de material radioativo no tempo $\displaystyle t=0$ seja $\displaystyle Q_{0}$ , temos

$\displaystyle Q(0)=Q_{0}$ .

Para resolver a Equação Diferencial Ordinária, basta separar as variáveis e aplicar o operador integral da seguinte forma:

$\displaystyle \int \frac{d \: Q(t)}{Q}=\int -r \: dt$ ,

que implica

$\displaystyle ln(Q(t))=-r \: t + C$ .

Além disso, cabe lembrar que $\displaystyle \ln(x) = \log_{e} x$ , que é definido como o logaritmo natural. Aplicando a exponencial nos dois lados da equação acima temos:

$\displaystyle Q(t)=e^{-r \: t + C}$ ,

na qual pode ser reescrita como

$\displaystyle Q(t)=e^{-r \: t } \times e^C$ .

Renomeando $\displaystyle e^C=C_{1}$ temos

$\displaystyle Q(t)=e^{-r \: t} \times C_{1}$ .

Como no tempo $\displaystyle t=0$ temos que $\displaystyle Q(0)=Q_{0}$ ficamos com:

$\displaystyle Q_{0}=e^{0} \times C_{1}$ ,

que implica em

$\displaystyle Q_{0}=C_{1}$ .

Logo,

$\displaystyle Q(t)=e^{-r \: t} \times Q_{0}$ .

Como a meia vida é o tempo necessário para que determinada quantidade de material radioativo decai a metade da quantidade original, temos que

$\displaystyle Q(\tau)=\frac{Q_{0}}{2}$ .

Assim, substituindo temos

$\displaystyle \frac{Q_{0}}{2}=e^{-r \: \tau} \times Q_{0}$ .

Dividindo os dois lados por $\displaystyle Q_{0}$ temos

$\displaystyle \frac{1}{2}=e^{-r \: \tau}$ .

Aplicando o logaritmo natural dos dois lados e usando a propriedade do quociente dos logaritmos fica-se com:

$\displaystyle \ln(1) - \ln(2)=-r \times \tau$ .

Como $\displaystyle \ln(1)=0$ temos que a meia vida $\displaystyle \tau$ é

$\displaystyle \tau = \frac{\ln(2)}{r}$ .

Portanto, espero que tenham se surprendido com a importância dos logaritmos não só para simplificação de contas, mas também nas aplicações do cotidiano. Grande abraço.

Publicado em 26/12/2019, em Curiosidades, logaritmo. Marcado com as tags John Napier, logaritmo, logartimos, propriedade dos logaritmos.

Logaritmos: contexto histórico e aplicações do cotidiano