Limites >

Exercícios resolvidos de limites – limites fundamentais

Exercícios resolvidos de limites – limites fundamentais

O primeiro passo ao resolver exercícios de limites é sempre aplicarmos o limite direto, mas muitas vezes chegamos a uma indeterminação. Assim, devemos buscar algumas alternativas afim de manipular a expressão e superar a indeterminação.

Neste post em que apresentamos Exercícios resolvidos de limites – limites fundamentais são muito úteis para conseguirmos eliminar a indeterminação e assim chegarmos a uma resposta.

Limites exercícios resolvidos – limites fundamentais

1) \displaystyle\lim\limits_{x\rightarrow 0}\frac{1-cos(x)}{x}

Como já comentamos no inicio deste post, o primeiro passo da resolução de um limite é aplicar o limite direto

\displaystyle\lim\limits_{x\rightarrow 0}\frac{1-cos(x)}{x}=\frac{0}{0} .

Como já suspeitávamos obtemos uma indeterminação. Para superá-la devemos manipular a expressão do limite. Visto que temos uma função trigonométrica no numerador, o limite tendendo a zero e a variável x no denominador. Tudo indica que podemos utilizar o 1º limite fundamental.

Para utilizar o 1º limite fundamental devemos ter a função seno no numerador, para isto propomos multiplicar a expressão do limite da seguinte forma:

\displaystyle\lim\limits_{x\rightarrow 0}\left (\frac{(1-cos(x))}{x}\cdot \frac{(1+cos(x))}{(1+cos(x))}\right )=\lim\limits_{x\rightarrow 0}\left (\frac{1-cos^{2}(x)}{x\cdot(1+cos(x))}\right ) .

Em seguida, devemos utilizar a identidade trigonométrica, \displaystyle sen^{2}(x)+cos^{2}(x)=1 onde obtemos

\displaystyle\lim\limits_{x\rightarrow 0}\left (\frac{sen^{2}(x)}{x\cdot(1+cos(x))}\right ) . 

Manipulando a expressão para ficar na forma do limite fundamental temos:

\displaystyle\lim\limits_{x\rightarrow 0}\left (\frac{sen^{2}(x)}{x\cdot(1+cos(x))}\right )=\lim\limits_{x\rightarrow 0}\left (\frac{sen(x)}{x}\cdot\frac{sen(x)}{1+cos(x)}\right ) ,

e utilizando a propriedade da multiplicação dos limites temos

\displaystyle \lim\limits_{x\rightarrow 0}\left (\frac{sen(x)}{x}\cdot\frac{sen(x)}{1+cos(x)}\right )=\lim\limits_{x\rightarrow 0}\frac{sen(x)}{x}\cdot\lim\limits_{x\rightarrow 0}\frac{sen(x)}{1+cos(x)} ,

onde chegamos ao resultado final ao aplicar o limite fundamental

\displaystyle \lim\limits_{x\rightarrow 0}\frac{sen(x)}{x}\cdot\lim\limits_{x\rightarrow 0}\frac{sen(x)}{1+cos(x)}=1\cdot\frac{0}{2}=0 .

 

2) \displaystyle\lim\limits_{x\rightarrow +\infty}\left (\frac{x+1}{x-1} \right )^{x+1}

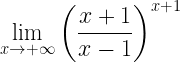
Observe que ao aplicar o limite direto obtém-se um outro tipo de indeterminação:  

\displaystyle\lim\limits_{x\rightarrow +\infty}\left (\frac{x+1}{x-1} \right )^{x+1}=1^{\infty} . 

Para resolver este limite utiliza-se novamente a propriedade da multiplicação, pois podemos abrir o limite em dois termos da seguinte forma:

\displaystyle\lim\limits_{x\rightarrow +\infty}\left (\frac{x+1}{x-1} \right )^{x+1}=\lim\limits_{x\rightarrow +\infty}\left (\left (\frac{x+1}{x-1} \right )^{x}\cdot \left (\frac{x+1}{x-1} \right )^{1} \right )= 

\displaystyle\lim\limits_{x\rightarrow +\infty}\left (\frac{x+1}{x-1} \right )^{x}\cdot \lim\limits_{x\rightarrow +\infty}\left (\frac{x+1}{x-1} \right ) .

O segundo limite é uma divisão de polinômios, assim podemos aplicar a técnica informal em que analisamos apenas o comportamento do termo de maior grau como:

\displaystyle\lim\limits_{x\rightarrow +\infty}\left (\frac{x+1}{x-1} \right )=\lim\limits_{x\rightarrow +\infty}\left (\frac{x}{x} \right )=1 .

Assim, devemos apenas nos preocupar com o primeiro limite. Para este limite propomos uma troca de variável y=x-1. Lembre que ao fazer a troca de variável temos sempre que analisar também o ponto limite.

Neste caso permanece tendendo a +\infty, pois quando x tende a infinito, y também tenderá a infinito. Assim, temos

\displaystyle\lim\limits_{x\rightarrow +\infty}\left (\frac{x+1}{x-1} \right )^{x}=\lim\limits_{y\rightarrow +\infty}\left (\frac{y+2}{y} \right )^{y+1} .

Novamente podemos abrir em dois limites como:

\displaystyle\lim\limits_{y\rightarrow +\infty}\left (\frac{y+2}{y} \right )^{y+1}=\lim\limits_{y\rightarrow +\infty}\left (\left (\frac{y+2}{y} \right )^{y}\cdot \left (\frac{y+2}{y} \right )^{1} \right )=

\displaystyle\lim\limits_{y\rightarrow +\infty}\left (\frac{y+2}{y} \right )^{y}\cdot \lim\limits_{y\rightarrow +\infty}\left (\frac{y+2}{y} \right )^{1}=\lim\limits_{y\rightarrow +\infty}\left (\frac{y+2}{y} \right )^{y}\cdot 1 .

Assim, temos 

\displaystyle\lim\limits_{y\rightarrow +\infty}\left (\frac{y+2}{y} \right )^{y}=\lim\limits_{y\rightarrow +\infty}\left (1+\frac{2}{y} \right )^{y} .

Perceba que este novo limite é muito semelhante ao 2º tipo de limite fundamental, na qual para utilizarmos o limite fundamental devemos fazer mais uma troca de variável, y=2t . 

Nota-se que o ponto limite permanece sendo +\infty, pois quando y tende a infinito, t também tenderá a infinito, assim temos 

\displaystyle\lim\limits_{y\rightarrow +\infty}\left (1+\frac{2}{y} \right )^{y}=\lim\limits_{t\rightarrow +\infty}\left (1+\frac{2}{2t} \right )^{2t}=\lim\limits_{t\rightarrow +\infty}\left (1+\frac{1}{t} \right )^{2t} .

Aplicando as propriedades das potências e potências de limite obtém-se:

\displaystyle\lim\limits_{t\rightarrow +\infty}\left (1+\frac{1}{t} \right )^{2t}=\lim\limits_{t\rightarrow +\infty}\left (\left (1+\frac{1}{t} \right )^{t} \right )^{2}=\left (\lim\limits_{t\rightarrow +\infty}\left (1+\frac{1}{t} \right )^{t} \right )^{2} ,

por fim basta aplicar o 2º limite fundamental para obter:

\displaystyle\left (\lim\limits_{t\rightarrow +\infty}\left (1+\frac{1}{t} \right )^{t} \right )^{2}=\left (e\right )^{2}=e^{2} .

Continue seus estudos de limites assistindo a resolução de alguns exercícios em vídeo clicando aqui. 

Publicado em 15/07/2017, em Limites.