Limite infinito – exercícios resolvidos

Limite infinito – exercícios resolvidos

Este post é dedicado a Limite infinito – exercícios resolvidos, ou seja, a resolução de alguns exercícios em que estão envolvidos limites dos tipos:

• Limites no infinito,
• Limites que tendem ao infinito.

Na resolução dos exercícios utilizaremos as propriedades dos limites, caso você ainda não os tenha visto este é o momento oportuno. 

Limite infinito – exercícios resolvidos de limites no infinito

Iniciamos com um caso bem simples de limite no infinito:

1) .

Como queremos saber o limite quando x tende a mais infinito, , ou seja, o valor de x é positivo, assim ao multiplicarmos um número positivo com um negativo, obteremos um número negativo.

Observe que o valor da constante 7 torna-se insignificativo, pois x assume valores muito maiores do que 7. Assim tem-se:

.

O próximo exercício é outro limite básico, entretanto que nos ajuda a entender limites mais complexos.

2) 

Neste exercício temos a variável x no denominador e devemos calcular o limite de x tendendo a menos infinito. Logo, temos a divisão de uma constante por um número cada vez maior. Assim, obtendo um número que se aproxima cada vez mais de zero.

Observe que o sinal do número do numerador é indiferente, o mesmo ocorre para a constante do denominador. Assim tem-se:

. 

Note que chega-se ao mesmo resultado se x tender a mais infinito. 

No exercício 3 aplicaremos um método rápido para achar os limites de funções racionais quando x tende ao infinito. 

3) 

O método rápido consiste avaliar o limite apenas nos termos de maior ordem do numerador e denominador, pois os polinômios comportam-se conforme o termo de maior ordem. Assim tem-se:

.

Repare que ao aplicar o método e ao simplificar obtemos o mesmo tipo de limite do exercício anterior,  

.

Exercícios resolvidos de limites que tendem ao infinito

Este tipo de limite nos exige analisar os limites laterais, pois no ponto em que devemos calcular o limite a função não está definida.

Novamente inicia-se com um exercício básico, que serve de base para outros exercícios.

1) 

Como queremos saber o limite quando x tende a 0, , o valor de x será positivo quando tendemos pela direita e negativo pela esquerda.

Para isto dividimos a resolução em duas partes:

Quando x tende pela direita,

Assim temos a divisão de uma constante por x positivo que tende a zero, onde x é um número muito pequeno em comparação a constante do numerador.  Assim o resultado da divisão é um número positivo cada vez maior

.

Quando x tende pela esquerda, 

No caso de x tender a 0 pela esquerda, x assume valores negativos. Isso é semelhante ao caso anterior, porém com sinal contrário 

.

Como os limites laterais são diferentes, o limite não existe no ponto x=0. Observe o gráfico que ilustra o comportamento desta função

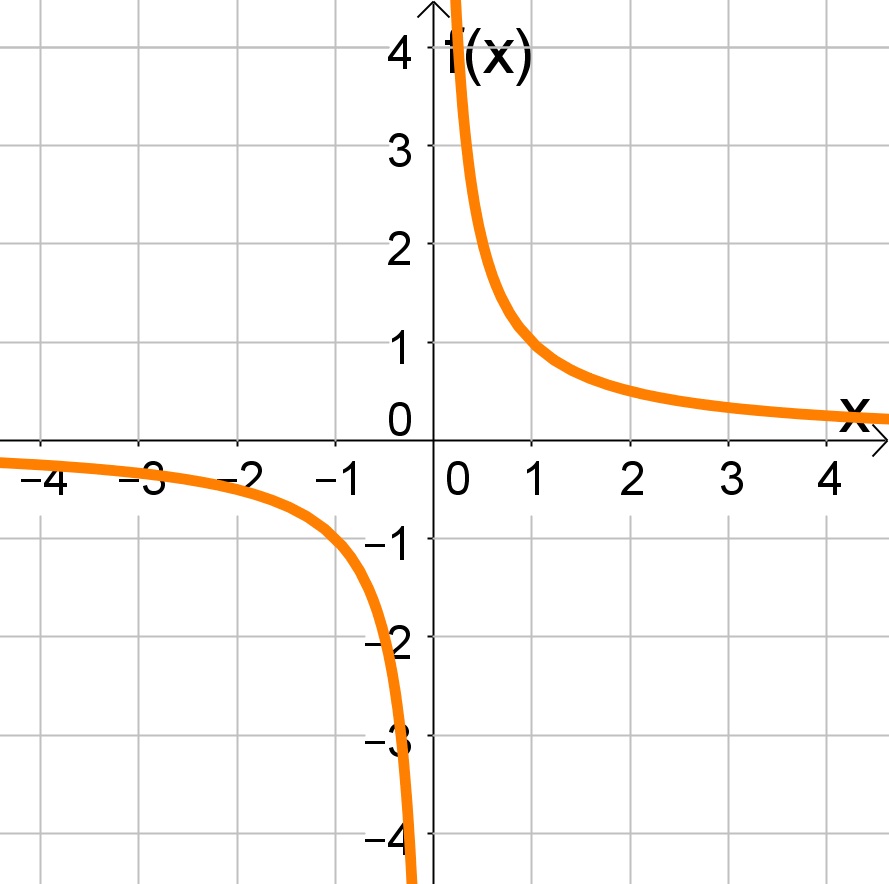
2) 

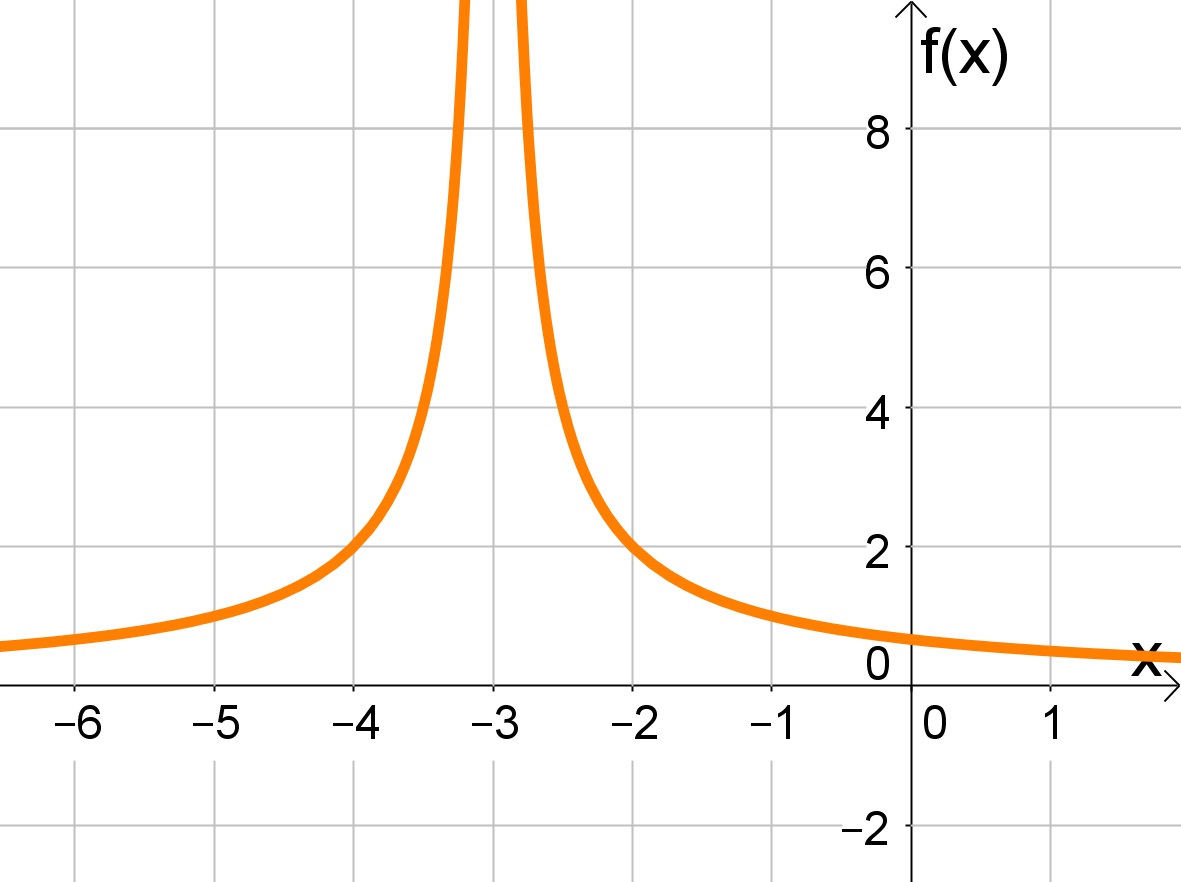
Neste exercício queremos saber o limite de f(x) quando x tende a -3, o valor de x+3 é positivo quando tendemos pela direita e negativo pela esquerda.

Entretanto, está em módulo, que produz apenas valores não negativos, logo o denominador resulta em valores muito pequenos positivos, indiferentemente se tendemos pela direita ou pela esquerda.

Portanto, tem-se os mesmos limites laterais e o limite existe 

.

Acompanhe outros exercícios deste tipo de limite no post em que resolvemos limites indeterminados.