Cálculo do volume dos sólidos de revolução com eixo deslocado – exercício resolvido

Neste post apresentaremos um exemplo do Cálculo do volume dos sólidos de revolução com eixo deslocado. Ou seja, quando o eixo de rotação não é o eixo x nem o eixo y. Este exemplo é uma resposta a uma dúvida levantada por um aluno do nosso site. Assim, nos dedicaremos hoje apenas a esta aplicação. Caso queira acompanhar a construção da fórmula do volume dos sólidos de revolução, clique no link.

Primeiramente recorde que a fórmula do volume dos sólidos de revolução é dada por

$\displaystyle V=\int_{a}^{b}\pi \big(f(x)\big)^{2}dx$ .

onde o volume está dentro do objeto gerado ao girarmos f(x) entorno do eixo x e x=a e x=b. Para o caso em torno do eixo y, a construção é análoga.

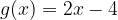Determine o volume do objeto gerado ao girarmos as funções $\displaystyle f(x)=2x^{2}-8x+4$ e $\displaystyle g(x)=2x-4$ entorno do eixo x=2 em 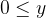$\displaystyle 0\leq y$ e ponto de intersecção das funções.

Primeiramente vamos construir o gráfico para uma melhor visualização do problema.

Cálculo do volume dos sólidos de revolução com eixo deslocado

Como o eixo de rotação é x=2, propomos uma transladação das funções duas unidades para a esquerda e, assim, teremos o problema como já sabemos calcular. Caso queira relembrar como se faz, clique aqui. Transladando

$\displaystyle f_{*}(x)=f(x+2)=2(x+2)^{2}-8(x+2)+4=2x^{2}-4$

$\displaystyle g_{*}(x)=g(x+2)=2(x+2)-4=2x$ .

Cálculo do volume dos sólidos de revolução com eixo deslocado

Observe que a transladação não alterará o valor do volume. Em seguida, devemos encontrar os pontos de intersecções, que são os pontos onde as duas funções são iguais.

$\displaystyle f_{*}(x)=g_{*}(x)$

$\displaystyle 2x^{2}-4=2x\:\Rightarrow\: 2x^{2}-2x-4=0$

Observe que temos uma função quadrática, em que devemos encontrar suas raízes. Iremos suprimir este cálculo, mas você pode optar pela forma que preferir. Eu optaria pelo Método da Soma e Produto, mas você poderia utilizar também a Fórmula de Bhaskara. Assim temos as raízes em $\displaystyle x=-1$ ou $\displaystyle x=2$ , onde descartamos $\displaystyle x=-1$ , pois não está no intervalo solicitado. Assim temos o ponto de intersecção (2,4).

O próximo passo é transformar as funções, pois temos as funções dependentes de x e precisamos que sejam funções dependentes de y. Para isto, insolamos a variável x

$\displaystyle y=2x^{2}-4\:\Rightarrow\: x^{2}=\frac{y+4}{2}\:\Rightarrow\: x=\sqrt{\frac{y+4}{2}}$

$\displaystyle y=2x\:\Rightarrow\: x=\frac{y}{2}$ .

Assim temos $\displaystyle f_{*}(y)=\sqrt{\frac{y+4}{2}}$ e $\displaystyle g_{*}(y)=\frac{y}{2}$ .

Finalmente, temos todas as informações para aplicarmos as integrais. Entretanto, só mais uma observação, note que $\displaystyle f_{*}(y)$ é maior do que $\displaystyle g_{*}(y)$ no interior do intervalo de integração. Portanto, devemos subtrair o volume gerado por $\displaystyle g_{*}(y)$ daquele gerado por $\displaystyle f_{*}(y)$ . Assim

$\displaystyle V=\pi\int_{a}^{b} \big(f_{*}(y)\big)^{2}dy-\pi\int_{a}^{b} \big(g_{*}(y)\big)^{2}dy=\pi\int_{a}^{b} \big(f_{*}(y)\big)^{2}-\big(g_{*}(y)\big)^{2}dy$ .

Aplicando temos

$\displaystyle V=\pi\int_{0}^{4} \left(\sqrt{\frac{y+4}{2}}\right)^{2}-\left(\frac{y}{2}\right)^{2}dy=$

$\displaystyle \pi\int_{0}^{4} \frac{y+4}{2}-\frac{y^{2}}{4}dy=\pi\left(\frac{y^{2}}{4}+2y-\frac{y^{3}}{12} \right)\bigg|_{0}^{4}=\frac{20}{3}\pi$

Assim obtemos o resultado desejado, caso você ficou em dúvida em algum passo, nos deixe seu comentário.

Cálculo do volume dos sólidos de revolução com eixo deslocado

Método exclusivo com explicações passo a passo, exercícios comentados e dicas práticas que você nunca viu na faculdade

Cálculo do volume dos sólidos de revolução com eixo deslocado – exercício resolvido

Determine o volume do objeto gerado ao girarmos as funções $\displaystyle f(x)=2x^{2}-8x+4$ e $\displaystyle g(x)=2x-4$ entorno do eixo x=2 em $\displaystyle 0\leq y$ e ponto de intersecção das funções.

Compartilhe agora mesmo:

Construindo gráficos de funções do segundo grau

Resolvendo Integral exp(x)cos(x) usando Integração por partes

Exemplo 6 – Inequação do 2 Grau

Para enviar seu comentário, preencha os campos abaixo:

Deixe um comentário Cancelar resposta

Seja o primeiro a comentar!

Método exclusivo com explicações passo a passo, exercícios comentados e dicas práticas que você nunca viu na faculdade

Damos valor à sua privacidade

Cookies estritamente necessários

Cookies de desempenho

Cookies de funcionalidade

Cookies de publicidade

Método exclusivo com explicações passo a passo, exercícios comentados e dicas práticas que você nunca viu na faculdade

Cálculo do volume dos sólidos de revolução com eixo deslocado – exercício resolvido

Determine o volume do objeto gerado ao girarmos as funções e entorno do eixo x=2 em e ponto de intersecção das funções.

Compartilhe agora mesmo:

Construindo gráficos de funções do segundo grau

Resolvendo Integral exp(x)cos(x) usando Integração por partes

Exemplo 6 – Inequação do 2 Grau

Para enviar seu comentário, preencha os campos abaixo:

Deixe um comentário Cancelar resposta

Seja o primeiro a comentar!

Método exclusivo com explicações passo a passo, exercícios comentados e dicas práticas que você nunca viu na faculdade

Damos valor à sua privacidade

Cookies estritamente necessários

Cookies de desempenho

Cookies de funcionalidade

Cookies de publicidade

Faça aulas personalizadas sobre conteúdos específicos de Matemática e Raciocínio Lógico

Determine o volume do objeto gerado ao girarmos as funções $\displaystyle f(x)=2x^{2}-8x+4$ e $\displaystyle g(x)=2x-4$ entorno do eixo x=2 em $\displaystyle 0\leq y$ e ponto de intersecção das funções.