aplicações >

Integração por Substituição Trigonométrica do primeiro tipo

Integração por Substituição Trigonométrica do primeiro tipo

O método da Integração por Substituição Trigonométrica do primeiro tipo é quando o integrando contém uma expressão algébrica do tipo  

\displaystyle \sqrt{a^{2}-x^{2}},

onde a é uma constante positiva. O método tem como base a substituição destas expressões algébricas por expressões trigonométricas. 

Em primeiro lugar, queremos relembrar as relações necessárias para substituição, que são a variável x, o termo dx e o termo raiz. O primeiro tipo tem como base a seguinte figura 

Integração por Substituição Trigonométrica - Tipo 1

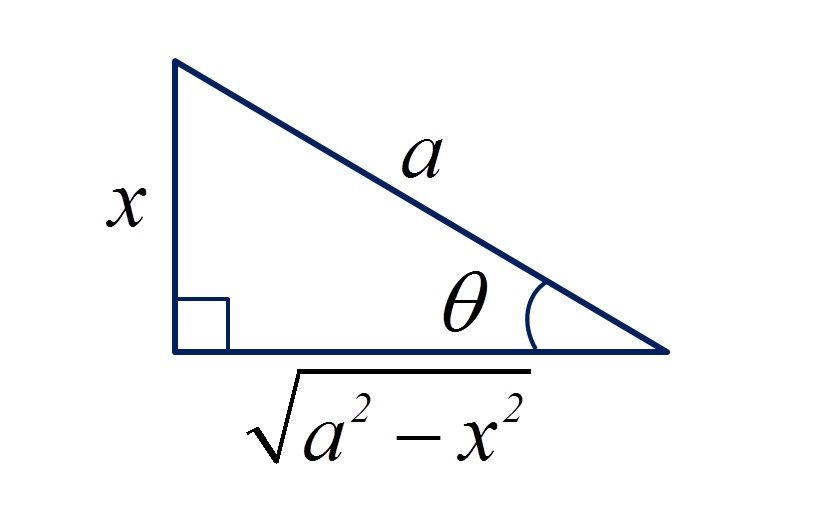
Assim, temos 

\displaystyle x=a\cdot sen(\theta )

\displaystyle dx=a\cdot cos(\theta )d\theta.

\displaystyle \sqrt{a^{2}-x^{2}}=a\cdot cos(\theta ).

Exercício: 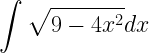\displaystyle \int \sqrt{9-4x^{2}}dx

O primeiro passo é observar que podemos reescrever o integrando da seguinte forma

\displaystyle \sqrt{9-4x^{2}}=\sqrt{4\left(\frac{9}{4}-x^{2}\right)}=2\sqrt{\frac{9}{4}-x^{2}}

desta forma temos que resolver a seguinte integral que está no formato da Integração por Substituição Trigonométrica do primeiro tipo

\displaystyle 2\int \sqrt{\frac{9}{4}-x^{2}}\;dx.

Assim, substituindo nas 3 relações apresentadas anteriormente temos 

\displaystyle x=\frac{3}{2}\cdot sen(\theta )

\displaystyle dx=\frac{3}{2}\cdot cos(\theta )d\theta.

\displaystyle \sqrt{\frac{9}{4}-x^{2}}=\frac{3}{2}\cdot cos(\theta ).

Substituindo na integral teremos

\displaystyle 2\int \sqrt{\frac{9}{4}-x^{2}}\;dx=2\int\frac{3}{2}\cdot cos(\theta )\frac{3}{2}\cdot cos(\theta )d\theta=\frac{9}{2}\int cos^{2}(\theta )d\theta.

A integral de cosseno ao quadrado é tabelada. Entretanto, iremos resolver como ela é calculada. Para isto, precisamos da seguinte relação trigonométrica  

\displaystyle cos^{2}(\theta )=\frac{1}{2}(1+cos(2\theta ))

Integrando nesta nova forma teremos 

\displaystyle \frac{9}{4}\int 1+cos(2\theta )d\theta =\frac{9}{4}\left (\theta+\frac{1}{2}sen(2\theta )\right )+C.

Agora temos que retornar ao problema em x. Para isto precisamos da seguinte relação trigonométrica  

\displaystyle x=\frac{3}{2}\cdot sen(\theta )\Rightarrow sen(\theta )=\frac{2x}{3}

\displaystyle sen(\theta )=\frac{2x}{3}\Rightarrow \theta=arcsen\left(\frac{2x}{3} \right)

\displaystyle \sqrt{\frac{9}{4}-x^{2}}=\frac{3}{2}\cdot cos(\theta )\Rightarrow cos(\theta )=\frac{2}{3}\sqrt{\frac{9}{4}-x^{2}}.

Além desta relações iremos precisar de 

\displaystyle sen(2x)=2sen(x)cos(x)

também substituindo temos 

\displaystyle sen(2\theta )=2sen(\theta)cos(\theta)=\frac{8x}{9}\sqrt{\frac{9}{4}-x^{2}}.

Agora temos todos os termos necessários para obtermos a resposta 

\displaystyle \frac{9}{4}\left (\theta+\frac{1}{2}sen(2\theta )\right )+C=\frac{9}{4}arcsen\left(\frac{2x}{3} \right)+x\sqrt{\frac{9}{4}-x^{2}}+C.

Assim, obtemos a resposta da integral proposta como exercício  

\displaystyle \int \sqrt{9-4x^{2}}dx=\frac{9}{4}arcsen\left(\frac{2x}{3} \right)+x\sqrt{\frac{9}{4}-x^{2}}+C.

Ou ainda, para deixarmos em um formato mais parecido com o enunciado da questão, podemos transformar o último termo da resposta

\displaystyle \int \sqrt{9-4x^{2}}dx=\frac{9}{4}arcsen\left(\frac{2x}{3} \right)+\frac{x}{2}\sqrt{9-4x^{2}}+C.

Acompanhe outros exercícios resolvidos neste link.

Publicado em 26/05/2019, em aplicações, Integrais. Marcado com as tags Integração por Substituição Trigonométrica, integral.